
摘 要: 针对图像中存在的对数螺旋线形状,提出了一种有效的对数螺旋线拟合方法。首先根据螺旋线的性质将已知图像中螺旋线的中心点约束在一个较小的区域内进行搜索,然后将从图像中获取的直角坐标系下的数据点通过坐标变换转换为能用直线形式表示的数据点,将对对数螺旋线的拟合转换为对直线的拟合。这一方法能快速、准确地拟合出图像中存在的对数螺旋线。
关键词: 坐标系变换; 旋转角; 对数螺旋线拟合
对数螺旋线(等角螺旋线)是一种在自然界中经常出现的曲线。由于它具有良好的几何、数学、力学及美学性质, 使得它在计算几何、工业造型、天文及气象研究、动植物研究等现代学科中得到了广泛的应用[1]。
对数螺旋线是一条古老的曲线,很早以前人们就在几何上对它进行了一系列的理论研究。卫星云图中台风的形成路径可以近似看作为一条螺旋线,进而根据在图中提取的部分曲线段所进行的螺旋线拟合来确定台风中心[2]。银河星系中的涡旋星系图像中,旋臂结构所构成的形状近似为对数螺旋线。由于星系演化和旋臂结构之间的相互影响,通过研究旋臂结构可以了解星系的演化[3]。
由于对数螺旋线是一条非闭合的曲线,不能简单地按照传统的闭合曲线拟合算法来对其进行拟合。目前可以通过将对数螺旋线的极坐标方程r=aebθ变换为lnr=bθ+lna的形式,也就是把局部的对数螺旋线上各点的坐标通过在不同的极坐标系下进行变换使其成为能最佳地满足直线方程的形式,可以通过最小二乘法[4]或Hough变换[5]来求得该直线方程的系数,进而拟合出最佳逼近的对数螺旋线。
这些方法都是通过不断扫描图像中的每一个像素点来假设其为对数螺旋线极坐标方程中的原点(x0,y0),然后在以该点建立的极坐标系中根据图像中所获取的对数螺旋线上的点来求出极坐标系下的极半径和旋转角。由公式求出的旋转角也只能是在0~180°的范围。而实际给出的对数螺旋线的旋转角度可以大于360°。
本文通过缩小极坐标原点的遍历区域来减少运算次数,达到提高运算效率的目的。同时考虑所获得弧段的极角大小在任意范围内。
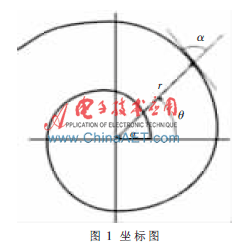




图6描述了对台风所形成的卫星云图进行处理的结果。图6(a)为真实卫星云图,图中含有螺旋云带。图6

本文通过约束对数螺旋线中心点的存在范围,将对数螺旋线的拟合转换为直线的拟合。实验结果表明,本文方法能够快速、较为准确地拟合出图像中存在的对数螺旋线。然而实际中,包含不同螺旋线的图像需要具体地分析,寻找更为合理有效的方法。
参考文献
[1] 游世辉, 李军. 对数螺线的应用研究[J]. 九江学院学报(自然科学版), 2005(3):6-9.
[2] 谢俊元, 艾早阳. 台风中心定位中的螺旋线自动识别算法[J].软件学报, 1997, 6(增刊):398-403.
[3] FRUHWIRTH R, STRANDLIE A. Helix fitting by an extended riemann fit[J].Nuclear Instruments and Methods in Physics Research(A), 2002,490(1-2):366-378.
[4] 刘凯, 黄峰. 无眼台风自动定位方法研究[J].信息与控制,2001,30(6):543-546.
[5] 孔秀梅. 形成期台风螺旋云带的提取、描述及中心定位的研究[D]. 天津:天津大学,2003.
[6] STEFANELL R, ROSENFELD A. Some parallel thinning algorithms for digital pictures[J]. Journal of ACM, 1971,18(2):255-264.