
摘 要: 一种快速序列穷举搜索蛋白质构像空间的算法。该算法利用二分技术将HP序列逐次分解,保存分解过程的中间结果,使搜索算法中所需的计算量大大减少。
关键词: 格子模型 完全二叉连接树 二分技术 HP序列
蛋白质是通过共价键将各种氨基酸的基本原子连接在一起的大分子。蛋白质的结构决定了其性能,因此理解蛋白质的结构和性能的关系至关重要。1973 年Anfinsen通过试验得出蛋白质的氨基酸序列在失性后可自发恢复其天然构像,并通过该试验得到二个结论:(1)对大部分单域蛋白质而言,编码蛋白质的氨基酸序列就可以决定它的空间构像;(2)蛋白质的天然构像选择的是能量最低的结构。
基于这一理论,人们提出了用全原子模型来进行蛋白质折叠模拟。该模拟涉及大量原子以及复杂的原子力场模型,所需的计算量庞大,目前的计算能力无法达到。格子模型是一种极为简化的蛋白质结构模型。在格子模型中,一个蛋白质的结构是由多个结点组成的连在二维或三维的正方格子空间的自回避行走所得的路径来表示。格子模型必须满足二个限制条件:(1)氨基酸序列中的共价键不能打断;(2)每个氨基酸占据一个格点,但一个格点不能被两个氨基酸同时占用。
由于组成蛋白质的氨基酸共有20种,所以长为N的蛋白质即有20N种序列,进行序列的穷尽搜索不现实。虽然氨基酸有不同的理化性质,但最重要的差异在于疏水性能。因此可以把氨基酸分成疏水氨基酸H和亲水氨基酸P二种。这样,格子模型在结构空间和序列空间都作了最大的简化,同时保留了蛋白质最基本的结构特性。天然蛋白质,特别是球蛋白,采用的都是致密的结构。所以,利用格子模型进行穷举搜索时,一般只搜索其致密结构。致密结构数与格子模型的格点多少、位置关系以及模型的维数有关。利用此模型可以对序列空间2N进行完备的描述及穷举化搜索,从而可以对天然蛋白质结构与序列的关系进行理论分析。很显然,穷举搜索会随着格点和维数的增加使计算量变得非常大。因此,本文构造一种有效的快速结构穷举搜索算法,大大降低了其计算量。经实验验证,该快速二叉连接树算法对长为N的HP序列的搜索,加速因子可达到2N。
1 快速序列搜索算法
HP序列是由疏水和亲水二种氨基酸组成。很明显,对长为N的HP序列可以用“0”(亲水残基)和“1”(疏水残基)字串表示:
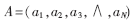
其中:A表示长为N的序列,ai表示第i个残基的疏水特性值。
HP序列折叠为某一结构的能量可采用氨基酸类型在结构中的埋藏度分布和表示:
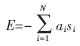
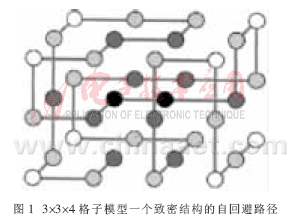
其中:si表示结构中第i个残基在格子模型中的埋藏度,如图1所示。结构格点可以分为四类:心点(图中用黑色表示)、面点(图中用黑灰色表示)、边点(图中用亮灰色表示)和角点(图中用白色表示),分别用四种不同的参数值来表示。为了简化能量计算,也可将心点和面点归为一类,边点和角点归为一类,用二个参数值表示。对本算法而言,使用何种表示方式对算法的计算量都不会有影响。通过这种表示,把能量的计算变成了二个向量的内积取负值。其表示公式为:
E=-A·S
在序列的穷尽搜索中包含大量的重复计算,如二个长为32的HP序列00000000111111111111111100000000和00000000111111110000000011111111。当针对同一结构序列进行计算时,前面16位的计算结果为重复计算。这时,可以把前面已经计算的中间结果存储起来,以便后面直接取用。亦即将16位后面的各位进行二分,计算时直接取用前面的结果。推广到一般的情形,可以在每一位的后面实行二分,以达到减少计算量的目的。将所有前面相同的字串只计算一次,并把结果存储起来,以便后面计算时使用。具体的二分演化模式如图2所示。
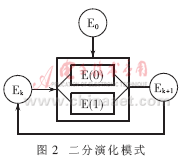
该二分演化技术是为了实现同步并行计算提出的,但是在这里也可用于快速算法设计。其中E0表示第0层,也即初始状态;第1层存在 “0” “1”二种状态,计算并保存其中间值;第2层以第1层的结果作为初值,经过二分和计算,其值作为第2层的结果保存。依此类推,第k层以第k-1层的结果作为初值,经过分解和计算,把结果作为第k层的值保存起来。演化到最后一层即得到了所需结果。
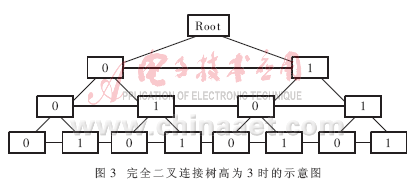
为通过此二分演化模式得到各种HP序列对致密结构的穷举搜索,可以采用完全二叉树来存储中间结果。同时还应注意,当后面的计算要用到前面的中间结果时,须进行序列搜索。然而,当搜索时间与计算时间相等时,则达不到减少计算量的目的。为了解决这一问题,将第k层的所有结点通过链表连接起来,计算第k层各结点的能量值时顺序计算,也就免去了搜索时间。为了便于中间结果的存储以及每一层结点顺序计算的方便,数据结构采用完全二叉树和每层结点连接起来的形式,本文称之为完全二叉连结树。
序列长度不同,所需构造的完全二叉连接树的高度也不同。图3为完全二叉连接树树高为3时的示意图。
在这种完全二叉连接树中,除了根结点和叶结点外,每个内结点应有一个指向父接点的指针、二个指向子结点的指针和一个指向兄结点的指针。每一层的最后一个结点的兄指针指向一个空指针。根结点的父结点指针和兄结点指针指向空指针,叶结点的子结点指针全部指向空指针。同时注意,为减少所需的存储量,可在第k层的中间结果计算完后,释放所有k-1层的结点,为第k+1层的结点开辟存储空间。
完全二叉连接树各结点的数据结构定义如下:

第0层为根结点,第1层为第一个序列值,对某一具体的结构序列,可以把能量计算公式改写为:
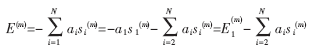
其中:m=1~M,表示第m个致密结构;E1(m)表示第1层结点的第m个致密结构对应的能量值;M表示该格子模型的致密结构数目。
对应的左子结点,由于a1为0,其能量值不用计算,直接补0;对应的右子结点,由于a1为1,其值为s1取负。将其中间结果E1(m)分别保存在第1层对应的序列值结点中。
同样,对于第k层的结点,其能量的计算要用到第k-1层的计算结果,公式为:
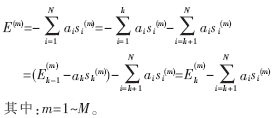
从公式中可知,要得到第k层的中间结果仅需计算aksk(m)的值。还可以发现,若k层中的结点为k-1层的左子结点且其对应的ak值为1,则该节点的中间能量值为上一层能量值减去sk(m);若为右子结点且其对应的ak值为0,则该节点的中间能量值直接赋值为上一层的能量值,并把得到的E1(m)值分别存储在第k层对应的序列值结点中。这一迭代计算公式一直做到完全二叉连接树的第N层,也就得到了所有序列对所有致密结构序列的能量值。
2 性能分析
从序列快速穷尽搜索算法可以看到,通过中间结点能量值的存储,大大减少了所需计算。对第k层结点而言,每个左子结点所需的计算量仅为一次加法,右子结点不用计算。第k层共有2k个结点,因此第k层的计算量为2k/2,则

3 实验结果与结论
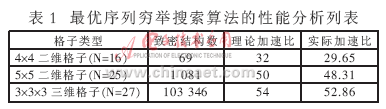
为了验证快速序列穷举搜索算法在实际应用中的有效性,将4×4和5×5二维格子模型以及3×3×3三维格子模型做了对比试验。从表1的实际加速比中可以看出,该算法在实际搜索过程中与理论上的加速比大致吻合。实际加速比略小的原因是由于完全二叉连接树各结点空间的开辟和释放以及一些辅助操作占用了一定的时间。
快速序列穷举搜索算法充分利用了二分演化模式技术,构建了完全二叉连接树的数据结构,从而将大量的重复计算简化到一次计算。而且利用二叉树二个子结点的特性,对值为1的结点仅需做一次加法,对值为0的结点不用计算,将二次乘法和二次加法变为一次加法,使得该算法对序列长为N的加速比达到2N。该算法为用格子模型对蛋白质结构进行理论分析提供了强有力的支持。
参考文献
1 Anfinsen C B.Principles that govern the folding of protein chains.Science,1973;181(96)
2 leach A R.Molecular Modelling:Principles and Applicants.Singapore:Longman,1996
3 Lau K F,Dill K A.Theory for protein mutability and biogenesis.Proc.Natl.Acad.Sci.U.S.A.1990;87(2)
4 Kloczkowshi A,Jernigan R L.Computer generation and enumeration of compact self-avoiding walks within simple geometries on lattices.Computational and Theoretical Polyer Science,1997;7(3)
5 Jensen l,Enumeration of compact self-avoiding walks. Computer Physics Communications,2001;142(1)
6 Cejtin H,Edler J.Fast tree search for enumeration of a lattice model of protein folding.J Chem Phys,2002;116(1)
7 王能超.同步并行算法设计.北京:科学出版社,1996