
0 引言
卫星任务设计过程中,如何实现对地面的特定位置和区域的有效覆盖是一个关键因素。随着卫星通信技术的发展,卫星点波束区域覆盖计算方法研究也取得了一定进展[1-3]。当卫星工作在正视模式下,波束中心与地面的交点与星下点重合,因此覆盖边界是卫星波束圆锥与地面的交线[2-3]。当有效载荷工作在侧摆状态时,需要对上述模型进行修正。一种模型是假设卫星侧视时在地面的投影是一个椭圆,椭圆长短轴和波束宽度以及波束中心星下偏移角?浊有关[4]。但因为地球表面为弧形,实际覆盖边缘不是规则的椭圆曲线,波束中心也并不是位于椭圆中心,因此这种假设误差较大。
本文中提出一种改进方法,通过卫星的侧视角度确定圆锥面,利用站心坐标系中波束的旋转角确定唯一的圆锥母线作为波束中心线,进而得到卫星波束中心与地球的交点,最终确定卫星覆盖范围。
1 侧摆载荷的波束与地面目标的关系
如图1所示,地球卫星位于S点,星下点位于G点, 卫星的点波束中心与地球表面相交于E点,其经度、纬度坐标分别表示为(Ls,Bs),(Lg,Bg),(Le,Be)。
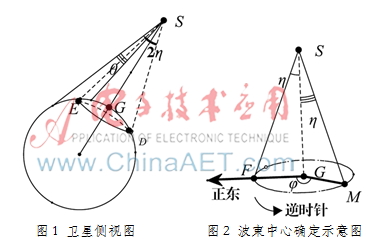
为了确定波束中心SE的方向,建立以星下点为原点的站心坐标系,正东方向(即与X轴平行的方向)所在平面SGF为参考平面,定义波束中心所在平面SGM(E为直线SM上一点)沿逆时针方向偏移MGF的角度为波束中心的旋转角度?渍,波束中心线SM(或者SE)偏离SG的角度为?浊,F、M为以点G为圆心,Re为半径圆上的点,如图2所示。其中:

则点F的站心坐标可表示为:
xgf=Re
ygf=0
zgf=0(2)
利用地固坐标系和站心坐标系的转换关系[6],可得地固坐标为(xef,yef,zef):
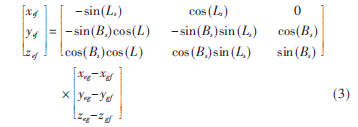
由卫星的经纬度可以得到星下点G的地固坐标(xeg,yeg,zeg)为:
xeg=Ncos(Bs)cos(Ls)
yeg=Ncos(Bs)sin(Ls)
zeg=Nsin(Bs)(4)
其中N表示零高程地球面半径。
此时可得到地固坐标系下星下点正东方向的向量GF:
GF=(xef-xeg,yef-yeg,zef-zeg)(5)
并将其作为卫星波束中心的偏移角度的参照。
2 载荷侧摆条件下覆盖范围求解算法
2.1 波束中心向量SM确定
如果点M在以点G为原点的站心坐标系内的坐标表示为(xgm,ygm,zgm),则:
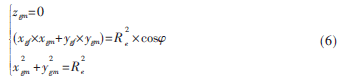
为了用角度得到唯一确定的M点,结合向量GF和GM外积n=GF×GM判别:即当?渍∈(0°,180°),n与站心坐标系的z轴同向,当?渍∈(180°,360°)时,与z轴反向,从而剔除与GF沿顺时针方向夹角为?渍的点M。得到确定的M点站心坐标后,将其转换成地固坐标(xem,yem,zem)。
2.2 确定波束中心点E
由点卫星经纬度,高度可以得到卫星在地固坐标系中坐标(xs,ys,zs),进而可得母线SM的参数方程:
x=xs+m(xem-xs)
y=ys+m(yem-ys)
z=zs+m(zem-zs)(7)
若把地球表示成一个平均半径为r0的标准球体,在地固坐标系中,点E的坐标表示为(xe,ye,ze),则:

将式(7)带入式(8)可得:
a2 m2+2a1 m+a0=0(9)
其中:
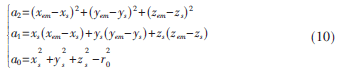
可解得:

为保证式(11)是实数解,要求星下偏移角?浊要小于地球半径角?籽。其中:

为了保证波束中心点和卫星是在地球的同一侧,所以上式中取m的较小值,最终可以得出波束中心点的坐标。将此计算结果转换为大地坐标系,即可得到卫星波束中心在地球表面的位置E(Le,Be,0)。
2.3 覆盖区域边缘点求解
在侧摆条件下,覆盖范围的边缘为不规则图形,按照上述求解点波束中心的方法,基于求解出的点波束中心,可以完成对边缘点的求解,最后完成对覆盖区域的计算。
3 仿真分析

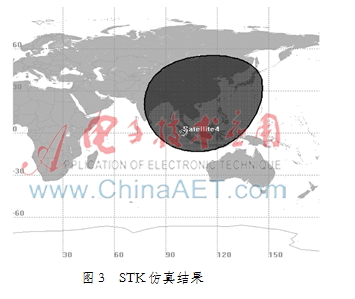

表1中列出了仿真的详细参数。图3是STK软件覆盖区域的仿真结果[9-10],图4是该算法通过MATLAB实现的区域覆盖仿真。图3与图4对比,说明该算法是有效的。
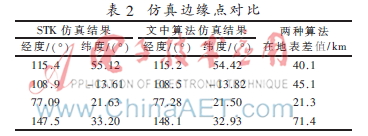
表2为分别选取上、下、左、右四个边界点进行的对比。数据对比表明,本文中提出的算法误差较小,在地表距离差值在72 km范围内。
4 结论
本文提出的波束中心确定算法,利用卫星旋转角度和斜视角度,通过简单的几何关系,最终确定卫星波束中心和地球的交点,从而确定卫星覆盖区域。这种算法简单,计算速度快、准确度高。因为波束形状的不同和波束中心点确定无关,所以此算法不仅仅适用于求解点波束的波束中心点,也适用于多种形状波束的波束中心点计算。
参考文献
[1] 徐慨,鲍凯,何爱林.卫星通信点波束覆盖算法研究[J].舰船电子对抗,2013,36(2):66-68.
[2] 李德治,宴朝阵,吕波.卫星点波束覆盖区域算法研究[J].载人航天,2009,15(4).
[3] 樊鹏山,熊伟,李智.载荷侧摆情况下卫星覆盖区域计算方法研究[C].2009系统仿真技术及其应用学术会议论文集,2009.
[4] 袁孝康.星载合成孔径雷达导论[M].北京:国防工业出版社,2003:42-44 .
[5] 白萌,李大林,陈梦云.卫星对地覆盖区域的融合算法研究[C].第二十三届全国空间探测学术交流会论文摘要集,2010.
[6] 郭福成,樊昀,周一宇,等.空间电子侦察定位原理[M].北京:国防工业出版社,2012:33-40.
[7] 翁慧慧.遥感卫星对地覆盖分析与仿真[D].郑州:信息工程大学,2006.
[8] 刘伟,孟新,胡钛.卫星对地覆盖的若干问题讨论[C].中国空间科学学会空间探测专业委员会第十八次学术会议论文集(下册),2005:370-372.
[9] 丁溯泉.STK在航天任务仿真分析中的应用[M].北京:国 防工业出版社,2011.
[10] 杨颖,王琦.STK在计算机仿真中的应用[M].北京:国防工业出版社,2005.