正交频分复用(OFDM)是一种多载波数字调制技术，其特点在于多个子载波在频率维度上可以相互正交、重叠，形成多个子信道，用于高速传递数据流。同时，OFDM系统能很好地对抗频率选择性衰落和窄带干扰，具有频谱利用率高、资源分配灵活、易扩展等优点，被认为是4G网络通信的核心技术，已经得到广泛应用与研究。
在OFDM技术中，如何合理地资源分配，提高系统性能，已成为研究热点。根据不同的优化目标，资源分配问题分为两种形式：速率自适应RA(Rate Adaptive)[1-3]问题和余量自适应MA(Margin Adaptive)[4]问题。RA问题的目标函数是最大化系统信道容量，其限制条件是总发射功率一定；MA问题一般是从能量有效性出发，其目标函数是最小化系统总发射功率，限制条件一般设定为用户速率或误码率低于预定值[5]。目前为止，采用相关优化算法求解RA问题，已经有一些相应的文献报道。文献[1]提出了基于比例公平的资源分配算法，利用最优的功率分配算法来实现用户之间的资源分配。然而，该算法利用迭代法求解优化问题中，求解空间和计算难度均非常大。文献[2]提出了一种最大最小化算法。然而，该算法是在平均功率分配的基础上建立的，忽略了信道质量实时变化的特性，在实际应用中具有一定的局限性。文献[3]利用注水算法进行功率分配，实现系统最大容量。然而，该算法忽略了用户之间传输速率的比例公平性，同时获得系统最优解的计算量较大。
本文在分析研究上述各种RA问题求解算法的基础上，提出一种基于信道聚合的OFDM自适应资源分配算法。利用子载波聚合分配的思想，在子载波分配过程中，兼顾用户速率比例的公平性，将子载波均匀地聚合成多个子载波组，分配给用户，提高系统容量，降低OFDM系统的峰均比（Peak to Average Power Ratio，PAPR）影响，有效地降低计算复杂度和获得最优解的计算时间。在功率分配过程中，基于遗传策略，利用改进的遗传算法进行子载波功率分配，实现系统总吞吐量的最大化。
1 系统模型
假设OFDM系统总的可用带宽为B Hz，共有K个用户，L个子载波，不同的用户之间不能共用同一个子载波，以免发生严重的干扰。整个频带被均匀地划分为多个子载波，即每个子载波的带宽为B/L Hz，将子载波均匀分组，分配给不同的用户。OFDM系统中子载波分组的示意图如图1所示。假定系统的子载波被分成N组，每组中有m=L/N个子载波，占用的带宽为B/N Hz。在一般情况下，分配的子载波数远大于用户数，因此假设子载波的组数N大于或等于用户数K。
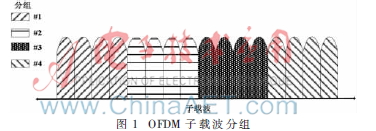
决策子载波分配的是基站。假定In代表任意一组子载波集合，n∈{1，2，…，N}；其中，第k(k=1，…，K)个用户在第i个子载波上的信道加性高斯白噪声为i，k，信道单位冲击响应为hi，k，第k个用户在第i个子载波上的发送功率为pi，k，每个用户总的最大可用功率为Pk。由文献[6]可知，通过信道聚合，第n组子载波分配给第k个用户，其等效信噪比SNR（Signed-to-Noise Ratio）为rn，k，即：
在迫零均衡器(Zero-Forcing equalization)的帮助下，将子载波聚合在一起，有效地利用子载波之间的相关性，降低OFDM系统中信号接收时PAPR的影响。同时，可以减小传输时延损耗。由香农定理可得，当用户k占据第n组子载波时，所得到的信道容量为：
设在一个时隙内，假定每组子载波只分配给一个用户，则系统总的容量为：
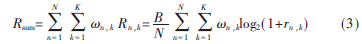
式中，n，k用来判断子载波n是否分配给用户k，若是则n，k=1，否则n，k=0。可以得到子载波分配矩阵：
根据假定每组子载波只分配给一个用户，可以得出子载波组分配矩阵满足如下的关系：
由文献[7]的分析可知，采用子载波聚合分配方式，可以将子载波均匀地聚合起来，分配给用户。当数据进行传输时，由于子载波组内的子载波频率是连续的，这使得在组内部传输的数据能更加高效地对抗PAPR的影响。同时，通过合理的分组，可以大幅提高子载波分配的速度，有效地降低计算复杂度和获得最优解的计算时间。
根据RA准则，假定网络是饱和的，即每个用户都有大量的数据需要进行传输，系统信道的总容量等于所有用户容量之和，其中每个用户的容量为已分配给该用户的所有子载波的容量之和。基于以上分析，优化问题可表示为：
在以上约束条件中，式(7)表示各个用户子载波上总传输功率不能超过用户本身限定的总功率值；式(8)表示各个子载波上的功率值需要大于等于0；式(9)和式(10)表示每个子载波只能被一个用户使用；式(11)是为了保证用户之间资源分配的公平性，其中预先设定的比例值。
根据RA优化问题建立的数学模型，可以看出自变量包含连续变量和离散变量，且限制条件很多，因此求解过程计算量很大且复杂度很高，很难快速找到最优解。为此，为了降低优化问题难度，本文采用两步法，先进行子载波分配。再进行功率分配，这样在优化过程中能有效地减少变量数目，大幅降低求解的复杂度。
2 分步优化资源分配算法
2.1 子载波分配
目前，OFDM的资源分配算法普遍的问题特点是求解空间大、计算量大且计算复杂度高，导致很难提出最优的分配方案。综合考虑，本文采用一种新的思路，在对子载波分配之前，采用分组的方式将子载波均匀组合在一起，并且把每组子载波看成是可分配的最小单元，优化分配给每个用户。一组子载波仅能分配给一个用户，但单个用户可以获得多组子载波。
首先，假定已知各个子载波上的传输功率，每个用户在子载波上的传输功率是一致的，则每个用户之间分配获得子载波数比例与用户的速率比例公平性系数近似相等。当第k个用户分配的子载波个数为Nk，即有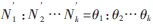
。然后确定哪组子载波分配给哪个用户，分配方法的目标函数是使系统性能损失最小，最终得出每个用户分配的子载波组数和子载波集合。在本文中，由于分配前将子载波进行等距离的分组，可分配的子载波组数已经大幅度降低。因此，本文假定各个子载波上的传输功率恒定，然后以一维穷举的方式完成子载波组分配。
2.2 基于遗传算法的功率分配
遗传算法[8]是在借鉴自然进化论和遗传学说的基础上，模仿自然选择和生物计划机制发展起来的迭代自适应概率性搜索算法，其主要特点在于模仿自然界生物进化机制，不依赖于梯度信息便可在较大的参数空间内获得全局最优解。本文在对各个用户的子载波分配完成之后，利用改进的遗传算法对各个用户在2.1节所得到的子载波进行功率分配，具体过程描述如下：
根据上一节子载波组分配完成的结果，用户k的子载波功率分配问题可以简化为
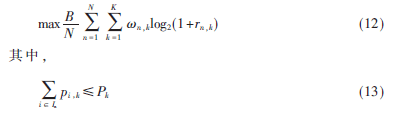
式中，rn，k是一个关于变量pi，k的函数。利用改进的遗传算法对上述优化问题进行求解，具体的分配原理如下：
(1)编码：随机产生一个具有多个元素的数列，其数列的元素为基因，代表一个子载波的功率值，取值范围为[0，1]，称一个数列为个体，每个个体都代表优化问题的一种解。
(2)种群初始化：随机产生M个个体，构成初始种群。
(3)计算个体适应度：将每个用户分配得到的子载波，根据目标函数公式计算得出用户的总速率，总速率的值作为个体的适应度值。若某个用户的子载波所对应的个体中基因的功率之和大于该用户总的发射功率，那么该个体的适应度等于种群中个体最小的适应度，将种群中所有个体的适应度升序排列，把种群中适应度最好的个体保存起来。
(4)选择：利用轮盘赌法，即基于适应度比例的选择策略，第j(j=1…M)个个体被选中的概率为第j个个体的适应度与所有个体适应度和之比，选出M个个体，组成交配对。
(5)交叉：设种群初始交叉概率为pc=0.7。在交配对所形成种群中剔出要变异的个体和最好的个体，对其余个体进行两两对应基因随机交叉产生新的个体，两两交叉后，把最好的个体放入种群中。
(6)变异：设种群初始变异概率为pm=0.01。根据种群初始设定的交叉概率，使用随机变异方式产生新的个体，每隔10代随机变异个体数就减1，直到为0，种群经过选择、交叉、变异运算之后，形成下一代种群。
(7)返回步骤(3)：重复迭代，直到个体的最大适应度的变化差值低于预定的最小值，最后输出用户间最优的功率分配及系统的总速率。整个算法流程见图2。
3 仿真分析
为了验证本文提出的自适应资源分配算法的性能，进行以下仿真分析。设定系统的可用总带宽为1 MHz，子载波数为64，将其分成16组，每组子载波数目为4，共有8个用户，用户的速率比例系数暂定为4:4:2:2:1:1:1:1，该速率比值可根据用户实际的需要进行调整。根据实际情况的特点，设定所有用户的最大限制功率都相等，即Pk相等。通过仿真将其与在子载波不分组的情况下利用遗传算法求解的资源分配算法（简称为不分组的遗传算法）、等功率分配算法进行比较。
图3为用户限制功率值Pk=1 W时，本文提出的算法与不分组的遗传算法适应度函数值进行比较。由图可知，在寻求最大适应度函数值的过程中，与不分组的遗传算法相比，本文提出的算法明显减少了遗传算法的迭代次数，提高了算法的收敛速度，同时本文算法获得最大适应度函数值明显大于不分组的遗传算法，提高了约0.2。
图4表示的是当用户总的限制功率值从1 W～10 W变化时，本文提出的算法与不分组的遗传算法、等功率分配算法的系统总速率的比较情况。由图可知，随着用户限制功率值的不断增大，本文算法获得的系统总速率值始终比不分组的遗传算法、等功率算法高。这是因为在本文所提的算法中，子载波被分组之后再进行资源分配、遗传算法求解时，其面对的优化问题的解空间得到有效减少，算法更容易逼近最优解。同时，分组的进行使得OFDM系统间PAPR降低，有效地提高了系统性能。
4 结束语
本文将信道聚合和遗传算法相结合，提出一种新的OFDM自适应资源分配问题。在子载波分配过程中引入分组的概念，信道组合操作简单，将复杂的求解问题简单化，更快地找到问题的优解。为了使资源分配的问题合理解决，先采用信道聚合的方式进行子载波分配，然后兼顾系统容量最大化和各用户之间公平性的需求，进行功率分配。仿真结果表明，本文提出的基于信道聚合与遗传算法相结合的自适应资源分配算法，在保证用户公平性的同时，有效地降低计算复杂度和获得最优解的计算时间，实现了OFDM系统总速率的最大化，为通信系统中自适应资源分配问题求解提供了一条有效途径。
参考文献
[1] SHEN Z K，ANDREWS J G，EVANS B L.Adaptive resourceallocation in multiuser OFDM systems with proportional rateconstraints[J].IEEE Transactions on Wireless Communica-tions, 2005，4(6)：2726-2737.
[2] CHO Y N，CHI W S.Low complexity subcarrier and power allocation algorithm for utility maximization in uplink OFDMAsystems[C].Proc of IEEE Transactions on Wireless Comm-unications，2008：1667-1675.
[3] MOHAMMED A L，PEI Xiao，MUHAMMAD A L，et al.Lowcomplexity subcarrier and power allocation algorithm for uplink OFDMA systems[J].IEEE Journal on Wireless Communications and Networking，2013，98(1):1-6.
[4] ZHANG G D.Subcarrier and bit allocation for real-time services in multiuser OFDM systems[C].Proc of IEEE International Conference on Communication，2004：2985- 2989.
[5] 汪照，李有明，陈斌，等.基于鱼群算法的OFDMA自适应资源分配[J].物理学报，2013，62(12)：128802.
[6] SHI T，ZHOU S，YAO Y.Capacity of single carrier systemswith frequency-domain equalization[C].Proc the IEEE 6th CAS Symposium on Emerging Technologies：Frontiers of Mobile and Wireless Communication，2004： 429- 432.
[7] Zhu Huiling，Wang Jiangzhou.Chunk-based resource allo-cation in OFDMA systems-part I: chunk allocation[J].IEEETransactions on Communications，2009，57(9)：2734-2744.
[8] 李鹤.比例速率约束下多用户OFDM系统自适应子载波和功率分配算法[D].长春：吉林大学，2007.
