
0 引言
准确而快速的故障检测和隔离可有效提升装备的任务成功率和装备完好率,同时降低保障规模和成本。为此,各型装备均提出了测试性要求,在研制过程中进行重点考虑。随着研究的日益深入和装备对测试性要求的不断提高,故障诊断技术被广泛应用在航空、航天、兵器等高精尖的新武器装备故障诊断上[1]。
作为故障诊断设计的核心,测试性建模与分析能够客观评估系统测试性设计水平,对于优化测试性设计方案、减少测试时间和费用、提高测试效率意义重大[2]。测试性模型的一种数学表达形式为D矩阵,在D矩阵中描述了故障-测试的相关性,是实现故障隔离、故障诊断树、排故逻辑的基础。
事实上在D矩阵中,要实现一个故障模式的隔离,并不一定需要所有的测试。即故障模式的测试向量不一定为测试项的全集。在故障隔离中,提前计算出每个故障模式的最优测试向量,可以在保证故障隔离准确度的前提下,提升故障隔离效率,缩短故障隔离时间,降低故障隔离成本。文献[3]提出了一种最少测试向量生成方法,可以准确计算出故障模式的最小测试向量[4],大大提升了故障诊断的效率。但是其求的是最优解,运算量大,计算时间长,适用于中小规模D矩阵的场合。
本文在文献[3]的基础上,针对大规模D矩阵的最优测试向量计算问题,提出一种新的最优测试向量计算方法,该方法采用最大分辨间隔思想求取近优解,在保证良好的优化效果前提下,大大缩减运算量。
1 测试向量
测试性建模[5]是使用标准有向图对产品的各层次模块、信号、故障模式、故障率、测试方法、测试点位置以及它们之间的逻辑关系进行描述的过程,逻辑关系就是建模对象的测试性相关信息。
测试性建模中,一种常用的数字表达方式为D矩阵,也称依存矩阵[6]。D矩阵是指反映测试与故障之间依存关系的矩阵,用于在采集各测试点的测试结果后,综合判断被测对象是否有故障或哪个组成单元发生故障,即完成故障隔离[7]。
定义D矩阵为D0:

其中,1≤i≤n≤p,1≤j≤m≤q,Fi表示的第i个故障模式,F0表示无故障状态,Tj表示的第j个测试。aij表示的是第j个测试与每个故障模式之间的相关性,当aij=0时,表示第i个故障模式和第j个测试不相关;当aij=1时,表示第i个故障模式和第j个测试相关。
在D0中,故障模式集为[F1 F2 … Fn],测试项集为[T1 T2 … Tm]。对于任一故障模式Fi,其测试向量为为实现该故障模式的诊断与隔离所用的所有测试组成的集合。测试向量表示为向量T=[Ti Tj … Tk],1≤i、j、k≤m。
2 测试向量的最优原则
在D矩阵中,对于单个故障模式而言,实现其检测和隔离过程中,有时不一定需要D矩阵中所有的测试的测试结果[8]。可实现故障模式的正确检测和隔离的分测试组成的向量为该故障模式的测试向量,测试向量的优化即为基于诊断需求和成本,计算得到相应测试向量的过程。衡量测试向量的最优原则包括:(1)测试数量最少;(2)计算测试向量时间最短;(3)测试成本最低;(4)测试时间最短;(5)实施困难程度最低;(6)资源占用最低。
实际使用过程中,最优原则可以采用这些原则的组合。
文献[3]中测试向量最优原则为首先考虑测试数量最少,其次综合考虑测试成本最低、测试时间最短。首先识别每个故障模式对应的测试数量最小的测试向量集合,然后综合测试时间、测试成本来确定最优测试向量。其确定的最优测试向量作为故障检测和隔离的判据,并将其转化为嵌入式诊断程序部署在产品的机内测试中。该方法能够实现以最优的测试费用、最少的测试准确找出故障源,从而提高电子产品测试性设计水平。
3 测试向量优化方法
本文提出的测试向量优化方法的测试向量最优原则为:首先综合考虑测试数量最少和计算测试向量时间最短,其次综合考虑测试成本最低、测试时间最短作为最优原则。
针对D矩阵D0计算最优测试向量,以Fi为例,计算其最优测试向量的步骤如下:
(1)针对D0矩阵中的第1个测试T1,计算[a11 a21 … an1]′中和ai1不同的个数,记为N1;针对第2个测试T2,计算[a12 a22 … an2]′中和ai2不同的个数,记为N2。如此,依次计算所有的测试T对应的N,得到集合{N1,N2,…,Nm}。从{N1,N2,…,Nm}中选取最大的Nk对应的测试Tk作为最优测试向量的第一个测试。当存在多个测试对应的N为最大时,意味着该故障模式可能存在多组最优测试向量,记最优测试向量的第1个测试集合为{Tk,Tl,…}。
(2)针对第1个测试集合中的每个测试,以Tk为例。在D0中,将Tk对应的列去除,同时将所有和ai1不一样的行去除,得到矩阵Dk:

(3)如果Dk中行仅剩F0,则转至步骤(2);否则,进入下一步。
(4)在Dk中,与步骤(1)中同理,依次计算Dk中所有的测试T对应的N,得到集合{N1,N2,…,Nm}。从{N1,N2,…,Nm}中选取最大的No对应的测试To作为最优测试向量的第2个测试。当存在多个测试对应的N为最大时,意味着该故障模式可能存在多组最优测试向量,记最优测试向量的第2个测试集合为{Tp,Tq,…}。
(5)和步骤(2)同理,针对第2个测试集合中的每个测试,以Tp为例。在Dk中,将Tp对应的列去除,同时将所有和ai1不一样的行去除,得到矩阵Dp。如此循环计算,直到矩阵中行仅剩F0。
(6)将上述步骤中最优测试向量的不同分支组合起来,形成备选的最优测试向量集合,有{[Tk Tp …],[Tk Tq …],[Tm Tq …],…}。
(7)从备选的最优测试向量集合中,选择数量最小的测试向量,得到最终的最优测试向量组,如{[Tk Tp …],[Tm Tq …],…}。
在计算某一故障模式的最优测试向量时,有时并非只有一组,可能存在多组测试向量的测试个数相等的情况。在最终的测试向量选择过程中,可参见文献[3]中的方法,选择最后的测试向量。
4 实验结果
4.1 仿真数据
随机生成不同大小规模的D矩阵,共生成了6个,分别为10×10、20×20、40×40、60×60、80×80、100×100。D矩阵中每个故障模式与测试的相关性服从{0,1}二项等概率分布,即为0或1的概率各为0.5。其中,10×10的随机D矩阵如图1所示。
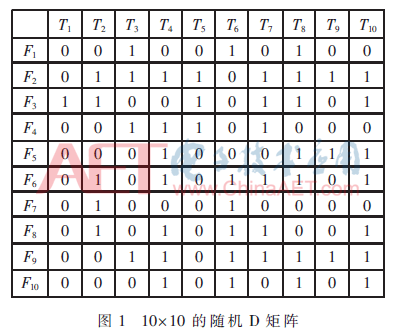
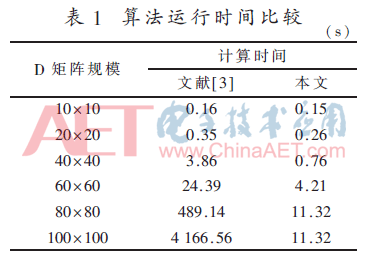
分别采用文献[3]和本文中方法对6组随机的D矩阵中每一个故障模式的测试向量进行计算。计算机性能为4核2.5 GHz CPU,6 GB内存,64位Windows 7操作系统。得到运算时间比较结果如表1所示。
同时,统计单个D矩阵中故障模式的平均测试数量和平均测试向量组个数。计算方法为:故障模式的平均测试数量=所有故障模式的测试向量计算结果中测试的总数量/故障模式数量,故障模式的平均测试向量组个数=所有故障模式的测试向量总组数/故障模式数量,以此衡量对测试向量的优化程度。得到测试向量优化程度比较结果如表2所示。

由表1可得,随着D矩阵规模的增加,文献[3]中方法的计算时间呈指数增长,而文本中方法的计算时间呈比例增加,D矩阵的规模越大,本文中方法的计算速度优势越明显。
由表2可得,两种计算方法得到的故障模式平均测试数量相近,文献[3]在平均测试向量组个数有较大优势。文献[3]方法为最优解,本文方法为近优解。
4.2 发动机停车电动装置实例
以飞机的发动机停车电动装置为对象,对两种方法进行比较。
发动机停车电动装置用于飞机的动力装置系统,其功能是关闭/打开发动机燃油开/关装置,发动机停车电动装置控制器通过接收飞机的停车开关的操纵指令,由控制器驱动电动装置控制发动机停车或工作,并通过HB6096总线输出工作状态信息。
通过中国航空综合技术研究所的测试性设计与分析系统TesLab-Designe V2.4,建立发动机停车电动装置的测试性模型[9]。测试性模型中共有174个故障模式、83个测试、28个信号。导出得到174×83的D矩阵。
使用中国航空综合技术研究所的嵌入式故障诊断软件TesLab-RT V1.1进行D矩阵整理后,得到精简后的D矩阵规模为81×74。
使用两种测试向量优化方法进行计算,比较结果如表3所示。

由表3可得,本文的计算时间远小于文献[3]中方法,两种方法得到的平均测试数量相同,仅在可供选择的测试向量组个数稍微少一些。
5 结论
实验结果表明,本文的测试向量优化方法具有计算速度快的优点,克服了已有的测试向量优化方法中存在的计算复杂度随着测试数目变大而呈指数增长的问题。较已有的方法,计算得到的测试向量的数量略大,属于近优的计算方法。
文献[3]中方法得到的测试向量中的测试数目肯定是最少的,测试成本是最低的,但是当产品的测试总数目较多时,计算速度较慢,适应于测试数目较少的情况。本文方法的计算速度非常快,但是计算得到的测试向量中测试向量的数目在某些情况下不是最少的,适用于产品的测试总数目较多的情况。
因此,当测试数目大于50时,可考虑使用文献[3]中方法进行最优测试向量计算;当测试数目大于等于50时,可考虑使用本文中方法进行最优测试向量计算。
参考文献
[1] 田恒,段富海,樊亮,等.基于测试性D矩阵的多故障诊断与维修策略研究[J].北京航空航天大学学报,2018,44(4):802-809.
[2] 郑应荣.系统级层次化测试性建模与分析[D].哈尔滨:哈尔滨工业大学,2014.
[3] Jiang Jueyi,Li Fan.Built-in test design and optimization method based on dependency model[C].Prognostics & System Health Management Conference,2016.
[4] 陶丽楠.面向固定型故障的测试向量生成与压缩方法研究[D].哈尔滨:哈尔滨工业大学,2012.
[5] 尹园威,尚朝轩,马彦恒,等.装备层次测试性建模分析方法[J].火力与指挥控制,2015,40(9):40-44.
[6] 杨其国.基于多信号模型的现场可更换模块测试性建模与分析[J].计算机测量与控制,2016,24(5):35-38.
[7] Tan Xiaodong,Qiu Jing,Liu Guanjun,et al.A novel approach of testability modeling and analysis for PHM systems based on failure evolution mechanism[J].Chinese Journal of Aeronautics,2013,26(3):766-776.
[8] Zhang Xishan,Huang Kaoli,Yan Pengcheng,et al.Hierar-chical hybrid testability modeling and evaluation method based on information fusion[J].Journal of Systems Engineering and Electronics,2015,26(3):523-532.
[9] 张弢,王金波,张涛.基于相关矩阵与概率模型的故障模糊诊断[J].系统工程与电子技术,2018,40(2):346-352.
作者信息:
蒋觉义1,李 璠1,李建宏2
(1.中国航空综合技术研究所,北京100028;2.中国电子信息产业集团有限公司第六研究所,北京100083)