
摘要:
1. 引言
散热器在计算时会出现误差,一般说来主要原因是很难精确地预先知道功率损耗,每只器件的参数参差不齐,并不是一样的,而且在芯片上各处的温度也是不同的。结果是,安全的裕度可能离开最优值很远。现在出现了很多功能很强的模拟仿真工具,因此有可能在预测功率损耗和热设计的校核方面做一些改进。然而,为了确保长期可靠性,运用复杂的限流技术可以更进一步地把最高结温(或者最大功率损耗)维持在一个预定的数值以下。 动态负载变化所引的任何热响应的改变都可以直接地进行测量,并且用闭路控制的方法来修正。
2. 热阻
发散出去的功率Pd 决定於导热性能,热量流动的面积以及温度梯度,如下式所示:
Pd=K*An•dT/dx (2.1)
式中 An 是垂直於热量流动方向的面积,K 是热导,而T是温度。可是这个公式并没有甚麽用处,因为面积An 的数值我们并不知道。对於一只半导体器件,散发出去的功率可以用下式表示:
Pd=∆T/Rth (2.2)
以及 Rth = ∆T/ Pd (2.3)
其中∆T 是从半导体结至外壳的温度增量,Pd 是功率损耗,而Rth 是稳态热阻。芯片温度的升高可以用式(2.2) 所示的散热特性来确定。考虑到热阻与时间两者之间的关系,我们可以得到下面的公式:
Zth(t)= Rth•[1-exp(-t/t )] (2.4)
其中(是所讨论器件的半导体结至外壳之间的散热时间常数,我们也认为 "Pd" 是在脉冲出现期间的散发出去的功率。那麽,我们可以得到:
∆T(t)=Pd• Zth(t) (2.5)
如果 Pd 不是常数,那麽温度的瞬态平均值可以近似地用下式表示:
∆T(t)=Pavg(t) •Zth(t) (2.6)
其中Pavg(t) 是散发出去的平均功率。作这个假定是合情合理的,因为瞬态过程的延续时间比散热时间常数短。由於一只MOSFET的散热时间常数为100ms的数量级,所以一般这并不成其为问题。热阻可以由产品使用说明书上得到,它一般是用“单脉冲作用下的有效瞬态过程的热阻曲线”来表示。

图 1 Zth(t) 瞬态热阻
3. SPICE 的实现
本文提出的模型使用一种不同的PSPICE 模拟量行为模型(ABM)建模技术。事实上,利用这种建模方法,使用者可以用数学的方法建立模型,不必使用更多的资源。
可以看到,由SPICE内的MOSFET模型,并不能以温度结点的形式直接得到温度。然而,可以用图4中所示的“窍门”来解决这个问题。
为了做到这点,把MOSFET M1表示成为一个普通的 Level-3 MOS模型 加上一个电路。 晶体管 M1 仅仅是“感知”温度,温度是指通用的SPICE变量“Temp”。为了评价温度对漏极电流的影响(由M1我们只能够确定在温度“Temp” 例如在 27 °C时,电流随著漏极电压的变化),增加了电路 G1 。这部份电路可以看成是电流受控制的电流产生器:
Id(G1)=Id(M1) • f(VGS,VDS,Tj,VTH,) (3.1)
在式(3.1)中的?数f的数学表达式可以从器件的输出特性通过内插法很容易得到。它与M1的模型有关,因而可以建立模拟量行为模型(ABM)。
4. 计算 Tj(t)
当大功率MOSFET工作在重复脉冲或者单脉冲的情况下,知道了平均功率损耗,然後将功率损耗乘以热阻 Zth(t),就可以得到模型的温度。在电路中,热阻 Zth(t)的数值是用电压来表示的,使用的符号为V(Zth(t))。参看模型G2,现们来计算M1的瞬时功率损耗:
Pd(t)=VDSG1(t) •IDG1(t) (4.1)
其中
IDG1(t)=IdM1(t) •f(VGS,VDS,Tj,Vth,) (4.2)
在式(4.1)中,Pd(t) 是“ELAPLA
CE”的输入量。 "ELAPLACE" 起积分的作用,於是得到消耗的能量 E(t);由此可以得到平均功率损耗如下
Pave(tk)= E(tk)/tk (4.3)
Pave(tk) 当然是与时间有关的,因为这个参数
是随著模拟仿真的进行而改变的。因此,平均功率损耗Pave(tk) 是变化的,它代表从模拟仿真开始到时刻tk这段时间的功率损耗的平均值。热阻曲线Zth(t) 可以以不同方式纳入到这个模型中。我们可以把单个脉冲响应用於Cauer或者 Foster网络。我们也可采用 a) 列表来表示, b)电压产生器 VPULSE,c) 一种激励电压产生器。芯片温度增高的平均值 ∆Tj-c(t)决定於Pave(t),再乘上Zth(t)。
因此Tj-c(t) 可以用下式表示:
Tj-c(t)= Pave(t) •Zth(t).+Tcase (4.4)
其中Tcase 取等於环境温度。
5. 模拟仿真结果及测量结果
在栅极驱动信号为不同类型的情况下进行了模拟仿真。下面图中的曲线是模拟仿真的结果。这些模拟仿真的结果是用新的SuperMESHTM STP14NK50ZFP 高电压MOSFET测量得到的,MOSFET是装在绝缘的外壳中。 这种MOSFET器件是用本公司专有的Mesh OverlayTM 技术的经过优化而制造的产品。下面是它的主要性参数:
|
BVDSS |
RDS(on) |
|
|
STP14NK50ZFP
(TO-220FP) |
> 500V |
< 0.38 W |
在很宽的温度范围上进行了测量,测量结果如图7示。

图 2 不同温度Tj时的输出特性曲线(实测结果)

图 3 在不同的Tj时的输出性曲线(模拟结果)
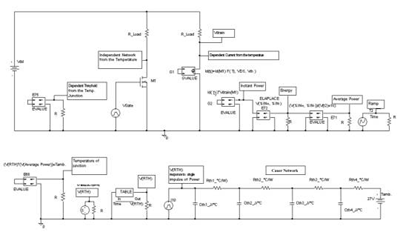
图 4 电路图
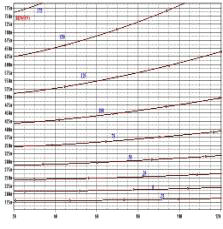
图 5 在10V时的RDS(on) (模拟结果)
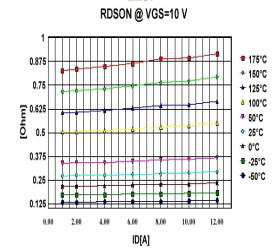
图 6 在10V时的RDS(on) (实测结果)

图7 在10V时的VDS(on) (模拟结果)

图 8 在 10V时的VDS(on)(实测结果)



图 9 (从上至下):
A) Tj 随时间的变化
B,C) 漏极电流
6. 结论
本文介绍了大功率MOSFET的一种新型的 PSPICE电路模型,其中包含热模型,利用这个模型,设计人员可以确定硅芯片在瞬变过程中任何给定时刻的平均温度。这个电路包含电气特性和热特性之间的动态关系。唯一需要的输入参数可以很容易地从制造商提供的产品说明书中得到。这些参数是热阻、 RDS(on) 随温度的变化,等等。 这个模型也可以用於其它的半导体器件,包括双极型晶体管。
可以相信,这里提出的模型可以用於对器件的热性能进行全面的分析,从而改进它的长期可靠性。
7. 致谢
本文作者借此机会感谢在Catania的MOSFET和IGBT产品技术和市场 部的宝贵建议和支持。
参考文
1. B.J. Baliga , Modern Power Device.
2. Dr. P. Türkes, Dr. M. M?rz, P. Nance, SPICE Models for SIPMOS Components Application Note.
3. Jon Mark Hancock Siemens Microelectronics A Hierarchical Cross-Platform Physics Based MOSFET Model for SPICE and SABER.
5. Dr. John W. Sofia Fundamentals of Thermal Resistance Measurement.
6. Dr. John W. Sofia Electrical Thermal Resistance Measurements for Hybrids and Multi-Chip Packages.