
0 引言
基于固定比率编码技术和请求重传机制的信道纠错技术已经很难满足下一代互联网日益增长的需求,因此无码率码被提了出来,它可以根据信道状态自适应调整码率,提高了信息传输的有效性。无码率码用一系列信息码生成一串无限长的编码位,接收端收集到一定数量的编码位后(原则上至少等于信息位数量)开始译码过程。如果不能从这些编码位中恢复出所有信息位,接收端就会收集更多的编码位再试。接收端持续这种方式直到所有的m个信息位得到恢复。如果在接收到n=m(1+O)个编码位后译码成功,则这个编码的译码开销为O。这样的方案被称为无码率,因为码率并不能预先固定,码率r=(1-ε)/(1+O)(ε为信道删除率),它会根据信道情况在0~1之间变化。无码率码非常适合于信息同时从一个发送端到多接收端的情况。
第一个实现无码率的是由LUBY M提出的LT码[1]:选择度值d(d的产生由给定的度分布函数决定),然后随机从K个信息位中选择d个信息位进行模二加,就可以生成一个编码位。译码端用低密度置信传播Belief Propagation(BP)算法恢复信息位。
AREF V等人提出了一种将空间耦合概念用于LT码的新的无码率码结构——空间耦合LT码Spatially Coupled LT(SC-LT)[2],并针对二进制无记忆对称信道(BMS)用密度演进来研究它的性能。在BMS信道此编码获得信道容量的一些必需条件也被推导出来。加入了预编码后的空间耦合无码率编码的性能也被大量研究[3-5]。大量的结果表明这些编码可以获得BEC信道的容量。这个结论也被文献[6]证明了。相比于传统LT码,SC-LT码要达到信道容量只需用非常简单的度分布(规则分布就足够了)[7]。
本文研究了SC-LT码在规则度分布、不规则度分布下的渐近性能以及有限信息长度下的性能,对两种度分布下的译码错误率以及译码复杂度进行比较。
1 基本概念
1.1 LT码
作为第一个实际可行的喷泉编码方案,LT码具有简单的编译码方法以及较小的译码开销和编译码复杂度,为喷泉码的发展奠定了基础。假设信源有K个信息位,编码过程如下:
(1)根据度分布随机的选择一个度值d,其中1≤d≤K。
(2)随机的从信息序列中选择d个信息位。
(3)假设Mi是信息序列的第i个信息位,那么编码符号输出为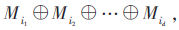 其中{i1,i2,…,id}表示从信息序列中随机选择的信息位的下标。
其中{i1,i2,…,id}表示从信息序列中随机选择的信息位的下标。
这个过程持续进行,直到接收的编码包数量能够使信息序列得到正确的译码。编码过程如图1所示。
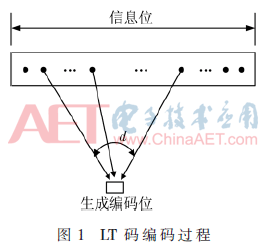
1.2 SC-LT码
SC-LT码对LT码的编码过程进行了改进,编码之前将K个信息位分割成L个信息集合,每个集合有m个信息位K=Lm。定义一个平滑参数ω,编码位被分成L+ω-1个集合。编码过程如下:
(1)随机选择一个整数j作为编码位的集合位置,j∈[1,L+ω-1]。
(2)从度分布R(x)中随机的选择一个度值d,其中1≤d≤mω。
(3)在信息集合[j-ω+1,j]中mω个信息位中随机选择d个信息位。
(4)将这d个信息位模二加就得到了编码位。
编码过程如图2所示。

这里要注意:对于位于编码集合[1,ω-1]∪[L+1,L+ω-1]的编码位来说,如果选择的信息位不在[1,L]范围内,编码器就认为该信息位无效(或者认为信息位的值为0)。
原则上,由这些mL信息位可以生成一串无限长的编码位。假设信息在一个删除率为ε的BEC信道上传输,用BEC(ε)来表示。接收端收集了一定数量的没有被删除的编码位后,(至少与信息位数目相等)开始用BP算法进行译码过程。如果收集到的编码位无法恢复所有信息位,则继续收集更多的编码位重试,直至译码成功。
随着收到的编码位数目的增多,每个编码所在集合的数目趋于预期估计值。因此可以假设他们的数目是一样的,用数字n来代表每个集合中的编码位数。但是这里需要注意,在属于编码位集合[1,ω-1]∪[L+1,L+ω-1]中的编码位数比n少。因为在编码过程中,属于这些集合中的部分编码位不与任何有效的信息位(即选择的信息位集合在[1,L]范围之外)相联系,这些编码位视为无效,被忽略。用oun表示每个集合的平均开销:

2 SC-LT码渐近性能比较
用BP译码算法译码时,可以用密度演进density evolution(DE)来研究SC-LT码在信息位无限长时的渐近性能[9-10]。
2.1 规则度分布的渐近性能
文献[7]中证明了在BEC信道下使用规则度分布的SC-LT码随着度值的增大可以接近信道的容量。规则度分布指的是度值选择一个固定值。显然度值的选择必须大于1,但度值的选择不宜过大,因为随着度值的增大,编码复杂度也会增大。
假设选择的规则度分布度值为d,SC-LT码的总开销为[5]:


对于BP译码算法,编码位的度值等于1是非常有必要的。使用固定的度值,除边界集([1,ω-1]∪[L+1,L+ω-1])中的编码位外,其他编码位集合中的编码位都有一个固定的度。一个足够大的?棕使得有效数目的度1编码位在边界集中。
由式(4)和式(6)即可计算出规则度分布的SC-LT码的译码性能。图3为规则度分布的SC-LT码在二进制删除信道下的性能展示。参数设置:L=256,ω=3,d=5。

2.2 不规则度分布的渐近性能
假设不规则度分布为R(x),SC-LT码的总开销由式(2)可推导为式(7):
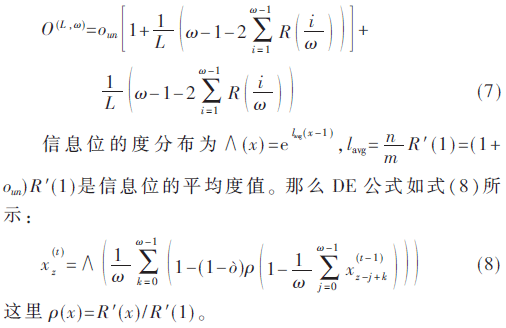
由式(8)和式(6)即可计算出不规则度分布的SC-LT码的译码性能。图4为不规则度分布的SC-LT码在二进制删除信道下的性能展示。参数设置:L=256,ω=3。不规则度分布采用文献[8]中介绍的。由图4可以发现使用不规则度分布有良好的性能,具有极低的译码错误率。

2.3 不同度分布的渐进性能比较
为了研究选择不同度分布对SC-LT码的性能的影响,下面在译码错误率和译码速度两方面进行比较。图5为译码错误率方面的比较。因为采用的不规则度分布的平均度值为5.87,所以将其与度值为5和6的规则度分布进行比较。

表1比较使用两种度分布时的译码速度,显示使用不同度分布的SC-LT码在不同开销下译码所需迭代次数。
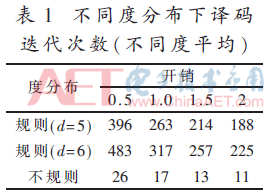
由图5和表1可以发现,使用不规则的度分布不会增加译码错误率,但是可以减少迭代次数,大大提升译码速度。
为了更直观地比较规则度分布与不规则度分布在译码速度和错误率方面的性能,在其他参数相同的情况下,令规则度分布的度值等于不规则度分布的平均度值5.87(当然在实际应用中规则度分布的取值不可能为小数,这里只是为了使比较更加直观)。
由图6和表2可以明显的发现,使用不规则的度分布与使用规则度分布相比译码错误率相差无几,但是前者有更快的译码速度。
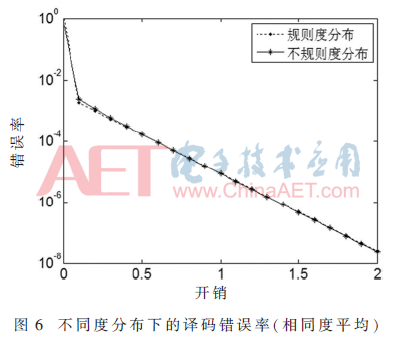

通过比较信息位无限长时两种不同度分布的渐近性能,发现使用不规则度分布具有更快的译码速度。
3 SC-LT码有限长性能比较
本小节研究SC-LT码在有限长度下使用两种度分布的性能比较。
3.1 有限长信息位性能分析
图7展示了在信息集合中的信息位个数m不同时,规则度分布SC-LT码的译码错误率比较,参数设置:L=256,ω=3,d=5。
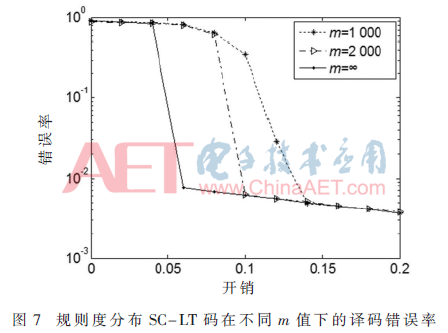
由图7可以发现,随着m的增长,SC-LT码以更快的速度接近渐近性能,那么当编码时信息集合中的信息位越多,就越能在低开销时获得低译码错误率。
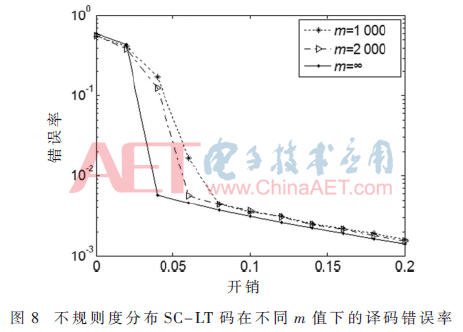
此规律同样也适用于使用不规则度分布的SC-LT码。由图8可以看出,随着开销的增大,有限长性能总会接近渐近性能。此外,由3.2节的结论可知,使用不规则度分布的SC-LT码不会带来译码错误率的升高。
3.2 不同的度分布的有限长性能比较
为了比较使用规则度分布和不规则度分布在信息位有限长时的性能,在信息位等长的情况下将平均度值为5.87的不规则度分布与度值为5、6的规则度分布进行对比,参数设置:L=32,ω=3。
图9表明,不论无限长还是有限长信息位,不规则度分布都比规则度分布具有更快的译码错误率下降速度。并且在有限长信息位时不规则度分布能以更快的速度接近渐近性能。

4 总结
本文研究了SC-LT码在两种度分布下的性能,分别在信息位无限长与有限长时进行比较,得出结论:(1)无论使用哪种度分布,编码时信息位集合中的信息位越多越能在低开销时获得低译码错误率,都以更快的速度接近渐近性能。(2)使用不规则的度分布后译码速度加快很多。而且在有限长信息位时能以更快的速度接近渐近性能。综合考虑译码错误率、译码速度以及译码开销,不规则度分布与规则度分布在译码错误率相差无几的情况下,前者能以更低译码开销接近渐近性能,并且具有更快的译码速度,优势明显,应用前景广阔。
参考文献
[1] LUBY M.LT codes[C].43rd Annual IEEE Symposium on Foundations of Computer Science,2002:271-280.
[2] AREF V,URBANKE R L.Universal rateless codes from coupled LT codes[C].2011 IEEE Information Theory Workshop(ITW),2011:277-281.
[3] SAKATA K,KASAI K,SAKANIWA K.Spatially-coupled precoded rateless codes[C].2013 IEEE International Symposium on Information Theory Proceedings(ISIT),2013:2438-2442.
[4] HUSSAIN I,XIAO M,RASMUSSEN L K.Design of spatially-coupled rateless codes[C].2012 IEEE International Symposium on Personal Indoor and Mobile Radio Communications(PIMRC),2012:1913-1918.
[5] AREF V.Spatially coupled codes for channel and source coding[D].Ph.D.dissertation,EPFL,Switzerland,2014.
[6] SAKATA K,KASAI K,SAKANIWA K.Spatially-coupled precoded rateless codes with bounded degree achieve the capacity of BEC under BP decoding[C].2014 IEEE International Symposium on Information Theory(ISIT),2014:521-525.
[7] AREF V.Rateless codes from spatially coupled regular-LT codes[C].2015 Iran Workshop on Communication and Information Theory(IWCIT),2015:1-6.
[8] SHOKROLLAHI A.Raptor codes[J].IEEE Transactions on Information Theory,2006,52(6):2551-2567.
[9] RICHARDSON T,URBANKE R.Modern coding theory[M],2008.
[10] KUDEKAR S,RICHARDSON T J,URBANKE R L.Threshold saturation via spatial coupling:why convolutional LDPC ensembles perform so well over the BEC[J].IEEE Transactions on Information Theory,2011,57(2):803-834.
作者信息:
陈 朝,毛明慧,陈 彬,赵卓亚
(中国地质大学(武汉) 通信工程系,湖北 武汉430074)