
0 引言
当前电力电子装置要求高效及高功率密度,上述要求推动了电力电子装置的高频化发展。由于逆变器在传动以及新能源领域得到了广泛的应用,逆变器的高频化越来越受到研究领域的重视。但逆变器的直接高频化带来了逆变器中高开关损耗和强电磁干扰的问题,而结合了软开关技术的软开关逆变器较好地解决了这个问题。
目前应用于逆变器的软开关技术中,按照拓扑的辅助缓冲电路中是否含有功率开关管可分为有源软开关逆变技术和无源缓冲软开关逆变技术[1]。有源软开关逆变技术通过在辅助缓冲电路中增加功率开关管的形式实现主开关管的软开关动作。一般采用有源软开关技术的拓扑存在逆变拓扑控制复杂、系统成本高以及辅助功率开关管的软开关问题,不利于工业应用[2-3]。而无源缓冲软开关逆变技术采用无源元件进行能量回馈,不仅能够实现功率开关管的软开关,而且成本相对低廉[4-5]。但是当前无源缓冲软开关逆变拓扑也存在着缓冲电路复杂,软开关实现过程中多组谐振造成的电磁噪声大以及能量缓冲过程造成的损耗大等问题[6-10],新型的无源缓冲软开关逆变拓扑仍在进一步研究完善。
文献[6]、[7]中的辅助缓冲电路采用变压器或耦合电感完成能量回馈;文献[8]中采用多个无源元件进行缓冲,导致拓扑较为复杂;而文献[9]、[10]中的拓扑虽然不使用变压器,但是在能量缓冲过程中多组谐振造成无源元件多次开关,产生的电磁干扰强,系统损耗高。因此,本文提出一种结构简单的无源缓冲软开关逆变拓扑,所提拓扑缓冲电路结构简单,拓扑成本较低,系统损耗低,在中小功率逆变场合具有良好的应用前景。
1 新型无源缓冲软开关逆变拓扑
新型无源无损软开关三相逆变拓扑结构如图1所示,其无源缓冲回路可分为三组,每相拓扑的辅助缓冲回路由2个电感、2个电容以及4个二极管组成,由于三相电路完全相同且独立可控,取一相电路进行研究,其单相电路如图2(a)所示。图2(a)中:E为直流电源,D1和D2为上下管换流二极管,D3~D6为辅助二极管,L1、L2为辅助谐振电感,C1、C2为辅助谐振电容,iC1和iC2为辅助谐振电容电流,iL1和iL2为辅助谐振电感电流,电容和电感的参考电压及电流方向均在图2(a)中给出。如图所示,当S1、S2开通时,谐振电感L1、L2限制开关管的电流快速增长,实现开关管的零电流开通;当S1、S2关断时,谐振电容C1、C2充电以限制开关管两端的电压上升率,实现开关管的零电压关断。


2 软开关逆变拓扑模式分析
所提拓扑一个开关周期可分为7个工作模态,分别如图2所示,本文根据回路换流模态图进行详细分析如下:
模式0 [~t0]:t0时刻之前,回路的初始状态为开关管S1处于导通状态,开关管S2处于关断状态,二极管D1导通,负载电流经二极管D1流向电源续流,其余所有二极管处于关断状态。谐振电容上的初始电压为vC1(t0)=0,vC2(t0)=E,谐振电感上的初始电流为iL1(t0)=0,iL2(t0)=0。开关管S1导通不流过电流,电路处于电能回馈状态,当开关管S1关断时本模态结束。
模式1 [t0,t1]:t0时刻,开关管S1关断,负载电流继续通过二极管D1进行续流,电路处于死区模态;由于二极管D1导通,开关管S1为零电压零电流关断;当开关管S2开通时,本模态结束。
模式2 [t1,t2]:t1时刻,触发开关管S2开通,负载电流开始由二极管D1换流至开关管S2,由于电感L2的存在,限制了开关管S2的电流上升率,开关管S2实现零电流开通,当谐振电感L2的电流上升至负载电流时,本模态结束,此时谐振电感上的电流为iL1(t0)=0,iL2(t0)=ia。
模式3 [t2,t3]:t2时刻,二极管D1的电流线性下降至零后自然关断,开关管S2的电流上升至负载电流,此时谐振电容C1、C2与谐振电感L1、L2进行谐振,当谐振电容C2的电压下降至零时,谐振电容C2和谐振电感L2谐振完毕,谐振电容C1和谐振电感L1继续谐振,但由于流过谐振电感L1、L2的谐振电流极小且时间极短,因此可以将其忽略得到本模式等效电路,当谐振电感L2和谐振电容C2谐振完成后,本模态结束。
本模态结束时,电感L2中电流达到恒定值,为:

模式4 [t3,t4]:t3时刻,谐振电容C2的两端电压下降至零后,二极管D2和二极管D4导通并分别流过谐振电感L2中谐振电流的一半;在回路中的电感L以及电容C取值极小的条件下,谐振能量极小, 而由于实际电路中的二极管、开关管存在不可避免的导通损耗以及线路损耗,谐振电感L1、L2的谐振电流将在开关管S2稳态导通期间很快被衰减到零,此时谐振电感L2和开关管S2仅流过负载电流ia,当开关管S2关断时,本模态结束。
模式5 [t4,t5]:t4时刻,由于谐振电感L2的电流不能突变,因此开关管S2关断后,二极管D4导通流过负载电流,谐振电容C1经二极管D4、D5、D6放电,电容C2经二极管D4充电,电容C2两端电压从零开始缓慢上升,开关管S2实现零电压关断,当谐振电容C2的两端电压上升到E,谐振电容C1的两端电压下降到零时,本模态结束。
模式6 [t5,t6]:t5时刻,当谐振电容C1的两端电压下降至零后,二极管D1开通流过负载电流,谐振电感L2中的残余能量经二极管D4、D6环流,由于实际电路中存在不可避免的线路损耗,谐振电感L2中的环流在上下管的开关死区内很快衰减至零,此后电路再次回到工作模式0,电路开始一个新的开关周期。
3 软开关逆变拓扑稳态特性
表1为新型无源软开关逆变器中不同元件的电压与电流应力。如表1中所示,开关管和二极管的电压应力与传统硬开关逆变器电压应力相当,且相较于传统的无源软开关逆变器,本拓扑中元件的电压应力较小;另外还可以看到,当电感和电容的参数取值极小时,电流应力很小接近于负载电流值大小,接近硬开关逆变器的元件电流应力值。

在SPWM调制策略下,开关管两端并联的电容限制了开关管关断以后其两端的最大电压变化率,开关管开通时的电流变化率由于电感的作用也得到抑制。开关管关断后其两端电压的上升率dv/dt、开关管开通后的电流上升率di/dt分别为:

由式(3)和式(4)可知,开关管关断之后其两端的电压变化率dv/dt和开关管开通后开关管的电流上升率di/dt及续流二极管中的电流下降率均可在电路参数选择时任意设置,同时可以看出当电容和电感取值极小时,上式两值可能相对较大,因此要综合考虑取值。另外由于变化率可以通过确定电容和电感参数进行确定,因此本拓扑结构可以有效降低主开关管的关断损耗以及续流二极管产生的反向恢复损耗,并可使回路产生的EMI进一步得到抑制。
设定开关管关断时的电压上升率(dv/dt)set为1 500 V/μs,逆变输入直流电压E=300 V,逆变输出负载电流最大值iamax=30 A,开关频率fS=16 kHz,逆变器上下开关管死区时间设定为4 μs。由式(3)得2C=ia/(dv/dt)set=20 nF,则选择谐振电容C为10 nF。谐振电感L的大小一方面要考虑到电流变化率,另一方面要考虑到电路中寄生参数的影响。由于工程实际应用中寄生参数难以准确估计,因此经过多次估算测试后来确定。Saber仿真时,选择谐振电感L为1 μH,谐振电容C为10 nF,满足要求。
4 仿真分析
图3为同等条件下硬开关工作时的开关波形图。从图中可以看到,硬开关状态下,开关管关断和开通时刻,开关管的电压上升率和电流上升率很高,开关管中产生的电压尖峰和电流尖峰较高。
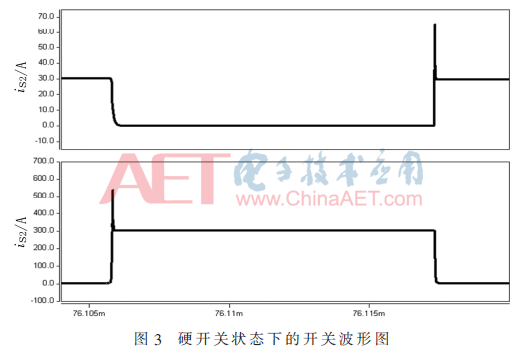
图4为本文所提拓扑的开关管开关时刻的动作波形图。
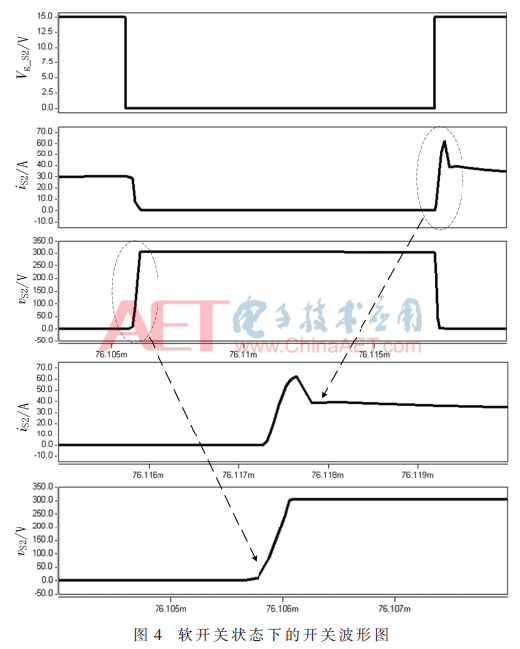
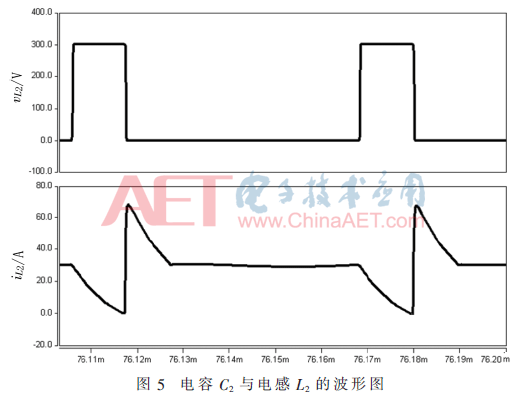
从图4中可以看到,当开关管开通时刻,其电流从零开始缓慢上升,开关管实现零电流开通;在开关管关断时刻,其电压从零开始线性上升,开关管实现零电压关断,且电压应力为电源电压,电流应力相对较小。图5为电容C2与电感L2的波形图,从模式5以及图4、图5中可以看出,在开关周期过程中,仅在开关管开通时刻产生一次谐振,经过此次谐振完成能量的转移,而波形图5中电容C2电压上升部分由于二极管钳位作用为线性上升,而电感电流的下降是由回路中的各种杂散损耗造成的。由仿真图可看出本文所提拓扑有效降低了系统损耗和电磁噪音。
5 结论
本无源软开关逆变器拓扑结构简单,通过合理设置谐振电容及谐振电感的参数,可实现开关管的零电流开通和零电压关断动作,系统中开关元件的开关损耗降低。本无源软开关逆变拓扑的辅助缓冲回路在实现软开关的能量交换过程中谐振次数少,降低了电压电流快速变化对周围元器件造成的不利影响,能量交换时谐振次数的减少有助于减少各元件的导通损耗。采用无源元件数目较少,减少了以往有源和无源软开关逆变回路中电容的数量和体积,逆变装置的体积和成本得到减少,具有良好的工业应用前景。
参考文献
[1] He Xiangning,CHEN A,Wu Hongyang,et al.Simple passive lossless snubber for high-power multilevel inverters[J].IEEE Transactions on Industrial Electronics,2006,53(3):727-735.
[2] 贺虎成,刘卫国,解恩.一种新型无刷直流电机谐振极软开关逆变器[J].电工技术学报,2008,23(12):99-106.
[3] CHU E,ZHANG X,SUN Q,et al.Three-phase double auxiliary resonant commutated pole inverter topology and analysis of its working principle[J].IET Power Electronics,2016,9(7):1536-1545.
[4] 邓焰,叶浩屹,何湘宁.完全的无源软开关功率逆变器研究[J].电工技术学报,2002(1):40-46.
[5] Yang Yuanyuan,Xu Weisheng.A simplified lossless passive soft-switching snubber for PWM half-bridge inverters[C].International Conference on Intelligent Computation Techno-logy and Automation,Changsha,China,2009:3-6.
[6] PENG F Z,Su Guijia,TOLBERT L M.A passive softswitching snubber for PWM inverters[J].IEEE Transactions on Power Electronics,2004,19(2):363-370.
[7] ZHANG H,WANG Q,CHU E,et al.Analysis and implementation of a passive lossless soft-switching snubber for PWM inverters[J].IEEE Transactions on Power Electronics,2011,26(2):411-426.
[8] 尹培培,洪峰,王成华,等.无源无损软开关双降压式全桥逆变器[J].电工技术学报,2014,29(6):40-48.
[9] 朱修敏,魏金成,魏力,等.一种新型PWM逆变器吸收电路[J].电子技术应用,2016,42(7):138-141.
[10] 王强,杨小葛,王天施,等.开关器件承受电压不高于直流电源电压的无源谐振极逆变器[J].中国电机工程学报,2017,37(15):4472-4482.
作者信息:
王晓标,邱佳雄
(东北大学 信息科学与工程学院,辽宁 沈阳110819)