
感应耦合电能传输技术(ICPT)以电磁耦合的方式实现供电部分与用电设备的非接触供电,消除了传统供电方式的一系列缺点,如导体裸露、机构磨损、接触电火花等,在各行业都有较高的应用价值。
多负载ICPT系统是指电能发射部分只有一组,而次级电能拾取部分有多组的ICPT系统。该系统能实现一个供电源对多个用电设备的非接触供电。如单轨铁路非接触供电系统[1-2]、非接触供电平台[3]等。随着科技的发展,多负载ICPT技术有着越来越广泛的应用。
目前已有一些对多负载ICPT系统的研究。参考文献[4]对多负载ICPT系统的电能发射和拾取线圈进行了优化设计,参考文献[5]中电能发射机构的磁芯对系统的电能传输效率和功率的影响进行了研究分析,得出系统传输功率的计算方法,参考文献[6-7]研究了多负载切换的控制方法和不同多负载的识别。这些文献中,主要是针对系统的传输功率进行研究,关于多负载ICPT系统效率的研究却比较少。而多负载ICPT系统的效率是影响其设计性能的一个重要指标。本文从多负载ICPT系统的等效互感耦合模型出发,针对多负载ICPT系统的传输效率进行分析。
1 多负载ICPT系统互感模型
多负载感应耦合电能传输系统主要利用电磁感应原理通过初级线圈和次级线圈之间的电磁耦合来传输电能,其原理图如图1所示。

互感模型是一种描述变压器初级与次级绕组磁场耦合关系的电路模型。该模型使用感应电压来描述变压器初级和次级绕组的耦合关系。基于互感模型的谐振电路分析方法,能够方便快捷地分析多负载ICPT系统输出效率。
图2给出了多负载ICPT系统互感模式的等效电路图。其中Vp是电网输入电压经过整流滤波电路和高频逆变电路之后的等效电压,Rp、Rs分别是初级线圈和次级线圈内阻,Lp、Lsi分别是初级线圈和次级线圈绕组电感,jω0MIp是初级电流在次级拾取机构中的感应电压,jω0MIsi是次级拾取机构中电流在初级发射机构中的反射电压。R1~Ri是次级拾取机构负载等效电阻。
为了便于系统参数设计和简化分析,本文设定所有拾取机构参数相同,即:
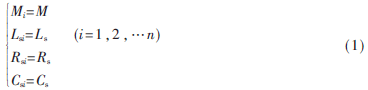
由于互感耦合率很低,因此为了提高系统的能量传输功率和效率,需要对ICPT系统初级和次级的励磁电感进行补偿。已有研究资料表明,多谐振补偿在ICPT系统功率传输和提高效率方面比单谐振补偿更具有优势[8]。图3是四种多谐振补偿拓扑结构图。
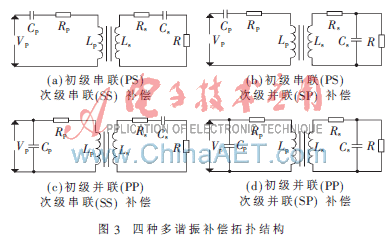
Cp、Cs分别是初级绕组和次级绕组谐振补偿电容。
2 系统补偿网络分析
由图3可知次级拾取机构串联电容补偿(SS)和并联电容补偿(SP)各自等效阻抗Zsi为:
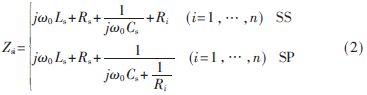
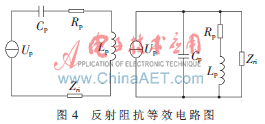
为降低电路计算复杂度,通常将系统次级拾取机构等效阻抗反射到初级绕组。图4是单个拾取机构到初级线圈的反射阻抗等效电路图,Zri是ICPT系统拾取机构到初级线圈的反射等效阻抗。
由图4可得初级绕组串联电容补偿(PS)和并联电容补偿(PP)的各自等效总阻抗Zp为:

电路谐振时,整个电路呈电阻性。因此根据谐振条件,可以计算出系统实现多谐振时初级补偿电容Cp满足表1中所示取值。

3 多负载ICPT系统效率分析
基于前文的分析与计算,得出多负载ICPT系统的效率计算公式(9),由此可以对多负载ICPT系统的效率和负载的关系进行分析。

由式(10)可以看出,ICPT系统的传输效率与系统的互感耦合值、系统工作频率和各个拾取机构的等效负载有关。可以设定f=20 kHz,M=10 μH,Rp=0.5 Ω,Rs=0.2 Ω。通过计算和MATLAB仿真,可以得系统效率与负载的关系曲线图如图5所示。

从图5可以看出,PSSS补偿时,系统采用恒流控制。对于完全相同的负载,在系统的工作频率、互感值一定的情况下,拾取机构的个数对系统的效率没有太大影响。负载的阻值较小时,对系统的效率影响较大,但是随着负载阻值的增大,系统的效率得到提高。同时,负载不同时随着负载阻值的增加,系统的传输效率同样得以提升。
4 实验验证与分析
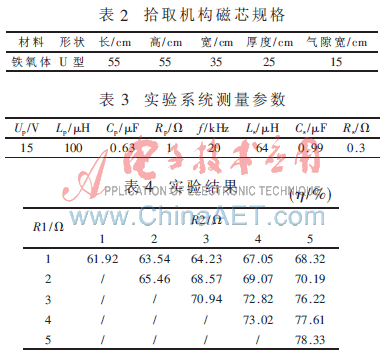
为验证上述关于多负载ICPT系统效率理论研究的正确性,以两个拾取机构为例,对理论分析部分进行实验验证。实验电路采用PSSS拓扑补偿结构的电压型多负载ICPT系统,拾取机构采用U 型磁芯,磁芯规格以及系统实验设定参数分别如表2、表3所示,系统控制采用恒流控制。实验结果如表4所示。
感应耦合电能传输系统的传输效率问题是该研究领域的一个热点。多谐振补偿能够大大提高系统的传输效率。多负载ICPT系统中初级补偿电容Cp值是一个很重要的参数,选择合适的Cp值才能保证系统有较高传输效率。本文通过对多负载ICPT系统的建模与分析,给出了多谐振时系统的效率计算公式和初级补偿电容Cp的选择方法。并且通过实验验证了PSSS补偿时的系统效率,证明了文中给出的多负载ICPT系统效率计算的正确性以及补偿电容Cp取值方法的正确性,对未来多负载ICPT系统的设计与优化具有一定的指导意义。
参考文献
[1] ELLIOTT G A J,COVIC G A,KACPRZAK D,et al. A new concept:Asymmetrical pick-ups for inductively coupled power transfer monorail systems[J].IEEE Transactions on Magnetics,2006,42(10):3389-3391.
[2] MATSUDA Y,SAKAMOTO H.Non-contact magnetic coupled power and data transferring system for an electric vehicle[J].Journal of Magnetism and Magnetic Materials,2007,310(2):2853-2855.
[3] 赵彪,冷志伟,吕良,等.小型非接触电能传输系统的设计与实现[J].电力电子技术,2009,43(1):49-51.
[4] 韩腾,卓放,刘涛,等.可分离变压器实现的非接触电能传输系统研究[J].电力电子技术,2004,38(5):28-29.
[5] 孙跃,卓勇,苏玉刚,等.非接触电能传输系统拾取机构方向性分析[J].重庆大学学报(自然科学版),2007,30(4):87-90.
[6] 杨民生,王耀南,欧阳红林.新型无接触电能传输系统多负载解耦控制研究[J].湖南大学学报(自然科学版),
2007,34(10):53-56.
[7] 孙跃,黄卫,苏玉刚.非接触电能传输系统的负载识别算法[J].重庆大学学报,2009,32(2):141-145.
[8] 周雯琪,马皓,何湘宁.感应耦合电能传输系统不同补偿拓扑的研究[J].电工技术,2009,24(1):134-139.