
摘 要: 在假设每次订货状况相同,且缺货造成的损失均摊到每次订货过程中去的情况下,根据物资流动过程中总量守恒建立等量关系式。总费用由N次订货总费用和总缺损费用两部分组成,而每次订货总费又由购物费、订货费、运输费、库存费四部分组成,再根据总生产量、总需求量等条件的约束,建立不等关系式。
关键词: 物资流通总量守恒;N次订货总费用;总缺损费用;优化分析
随着科学技术的发展,社会生活的进步,商业公司订货时有着越来越多的选择,如何制定订货策略成了商业公司生产销售环节中很重要的一环,因此对商业公司订货问题的研究对商业公司的运营具有重要的意义。
1 订货问题叙述
某商业公司管理着5个仓库(B1~B5)和8个分店(C1~C8),主要经营10种物资,而这些物资全部向3个工厂(A1~A3)进货。公司的工作流程是根据8个分店的销售需要,先向工厂订货,然后将各种物资运送到仓库,再由仓库运送到分店进行销售(分店只消耗物资,不储存物资)[1]。
各个工厂生产10种物资的全部或部分物资的年产量和各种物资单价、每个工厂到每个仓库的运输单价及每个仓库的容量参见参考文献[1]。同种物资在不同的仓库的库存费一样,而不同物资的库存费是不同的。每种物资有着自己的体积,物资的库存费与单位占用库容、5个仓库到8个分店的运输单价及8个分店对物资的年需求量参见参考文献[1]。
公司每次订货都会有其他的各种花费,称为订货费,设公司每次的订货费为1万元。另外,一次订货可使用的流动资金上限为100万元,如果进行销售时允许缺货,但缺货的损失费是存储费的2倍。建立模型解决公司一年之中应该怎样组织订货,并使得总花费最少。
2 问题分析
要确定组织订货的方式,首先从一次订货进行考察,一次订货总费用分为五部分,分别为运输费、购物费、定货费、库存费、缺损费[2]。对上述五部分分别进行分析建立模型,并结合题意,列出多个等量关系、不等关系作为约束条件,进而求得总费用的模型,编程求得最佳方案使得总费用最少。
3 优化模型建立
在建立模型时,为使模型简单、易于理解、便于计算,作如下假设:
(1)假设每次订货情况完全一致,且每种货物出售状况均为稳定售出[3];
(2)假设仓库在每一次订货后各种货物均匀减少,且同时售完,但下一次货物会立即补充,刚好售完与立即补充之间的时间间隔很短,可忽略不计;
(3)假设每件产品库存不到一年均按照一年的库存费用算,缺损费每次订货均摊。



每次订货过程中3个工厂运往5个仓库和5个仓库运往8个分店的运输方案分别如表1、表2所示。
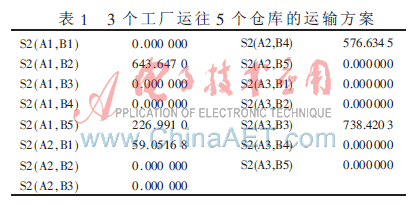
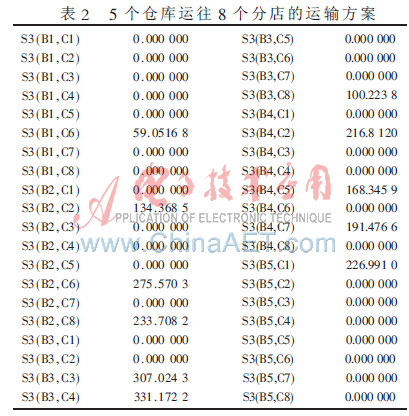
实际问题中每一次的订货状况不一定相同,且并非周期性订货,即存在出售高峰期和出售低谷期。但在本文假设条件下,即每次订货状况相同,将复杂问题简单化,分析得到的订货方式能够在很大程度上解决问题。
参考文献
[1] 公司订货问题.MATLAB中文论坛:http://www.ilovematlab.cn/thread-83116-1-1.html.
[2] 杜廷松.订货问题的一个最优存储模型[J].商场现代化,2007(500):11.
[3] 史玉敏.基于价格有折扣的零售商订货问题[J].物流技术,2008,27(8):102-104.