新型非线性PID控制器仿真研究
作者：李东海1 吴勇强1 李燕茹2
发布日期：2009-07-22
摘 要： 提出一类非线性PID控制器结构，并进行了控制系统仿真研究。结果表明，非线性PID控制器具有优良的动态性能，且参数整定比较简便，显示出良好的工程应用前景。
关键词： 非线性控制 PID控制器 系统仿真
PID控制器原理简单、使用方便、适应性强，在控制工程中获得了广泛应用。但对于非线性对象，PID控制器并不总能得到满意的结果。对非线性较强及经历大范围变化的系统，问题更加严重。非线性控制方法如微分几何方法和逆系统方法可以获得优良的控制性能，但需要对象的数学模型。而建立工业过程的数学模型在许多情况下是比较困难的。如果在传统PID的基础上加以改进，使其能够对某些非线性对象的控制取得较好的控制效果，无疑具有重要的工程价值。基于这一想法，本文提出一类非线性PID控制器，简称NLPID。通过若干非线性控制系统仿真研究，证实了这类非线性PID控制器的有效性。
1 非线性PID控制器结构
工业控制系统常见的PID控制器输入输出关系为：
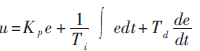
可见其输出u是
的线性组合。现假定非线性PID控制器输入输出关系为：
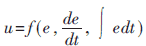
但由于控制器函数无法获得或非常复杂，不能写成简单实用的数学表达式。为书写方便，将控制器函数的三个变量分别写作x1、x2、x3,依据泰勒定理可用
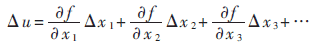来近似。如何近似控制器函数f，考虑以下几点：
(1)对于控制器函数f,假定x1＝0,x2＝0,x3＝0，则u＝0。常规PID控制器函数显然满足此假定。
(2)控制器函数要遵循控制系统的负反馈原理，所以在泰勒展开中只取奇次幂项。
(3)为保证控制器的简单性，最高幂项取为三次。
所以PID控制器函数表示为：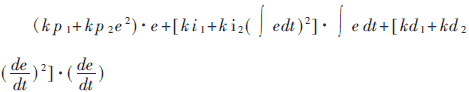 
为了和其他类型PID相区别，在本文中我们把这种非线性PID称为NLPID，如果kp2＝0，ki2＝0，kd2＝0,则NLPID就等同于常规PID。
2 仿真研究
为了验证非线性PID控制器的效果，采用两个不同的非线性被控制对象进行控制系统仿真研究。由非线性PID构成的控制系统结构图如图1所示。
2.1仿真研究1
设被控制对象的数学模型为：
y″+3y2y′+2y3＝u
为比较NLPID与PID对这一对象的控制性能，在小偏差的范围内调整各自的控制器参数，达到近似的性能指标，再逐渐增大给定值，比较两个系统输出的性能指标。
r＝10u(t)时整定PID及NLPID控制器参数如下：
PID参数为：kp＝20,ki＝250,kd＝20;
NLPID参数为：kp1＝20，kp2＝0，ki1＝2，ki2＝2，kd1＝20，kd2＝0。
对不同的给定值，PID与NLPID调节性能指标如表1所示。由表1数据分析可知，当给定值在一定范围内增大时，由PID构成的控制系统输出曲线性能指标变差，而NLPID控制输出曲线的性能指标变化较小，保持小偏差整定时的调节效果。两个控制系统在不同给定值时输出曲线比较见图2。
2.2 仿真研究2
设被控制对象由一限幅环节与传递函数
构成，限幅环节的输入输出表达式为：
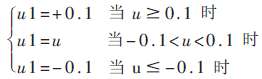
设u为输入，u1为输出。
同仿真研究1，r＝10u(t)时，分别整定PID及NLPID的参数如下：
PID参数：kp＝0.4,ki＝0,kd＝2.4;
NLPID参数：kp1＝0.4,kp2＝0,ki1＝0,ki2＝0,kd1＝2.4,kd2＝0.4。
对不同的给定值，PID与NLPID调节性能指标如表2所示。通过对表2数据的分析，可以得到与仿真研究1相同的结论，即:
当给定值在一定范围内增大时，由PID构成的控制系统输出曲线性能指标变差，而NLPID控制输出曲线的性能指标变化较小。两个控制系统在不同给定值时输出曲线比较见图3。
仿真研究表明，本文提出的非线性PID控制器对于某些被控制对象具有比常规PID更好的调节性能及更大的稳定域。当设定值r在一定范围内增大时，常规PID的控制效果明显变差，而NLPID仍保持较好的控制效果。
关于非线性PID控制器理论问题，如从理论上分析其具体的数学表达形式及其适用范围、参数整定规则等，有待于进一步的深入研究。
参考文献
1 古钟璧，王 苇，王祯学.大滞后生产过程的智能式补偿预测控制.自动化学报，1995；21(4)：494～497
2 李东海.非最小相位控制系统的智能设计(博士学位论文)
3 李清泉，郭 莉.智能PID控制器.自动化学报，1993；19(3)：336～339
