
摘 要: 包络对齐是逆合成孔径雷达(ISAR)平动补偿的关键技术,是图像重构的基础。依据设备所使用包络对齐方法,在积累互相关法的基础上进行算法改进,提出迭代相关对齐法。不同于原方法,迭代相关法使用平均距离像作为参考包络对各次回波作相关对齐,并进行多次迭代,直至收敛,有效地防止对齐漂移和突变误差的发生,从而保证了包络对齐的精度和稳定度。仿真结果表明,该方法能显著提高包络对齐精度从而提高ISAR成像质量,且运算量增加不大。
关键词: 包络对齐;ISAR;迭代相关
逆合成孔径雷达(ISAR)成像技术是在合成孔径雷达技术上发展起来的。ISAR成像系统为雷达静止、目标运动的成像系统,不同于传统雷达,它是一种高分辨率成像雷达,能够远距离获得非合作运动目标的精确图像[1]。ISAR成像前需对运动目标进行平动补偿来抵消每次回波相对于雷达的平动变化,从而只保留目标的转动(即转盘模型),此时只需要进行相应的成像算法即可得到目标图像。本文主要讨论包络对齐的方法,包络对齐的作用就是针对距离单元进行校正,前提是将同一散射点的子回波调整到同一距离单元中,否则会严重影响成像的质量,因此包络对齐是ISAR成像中的关键技术。
1 ISAR成像原理
成像雷达分为两类:合成孔径雷达(SAR)和逆合成孔径雷达(ISAR)。SAR通常安装在飞机、卫星等运动平台上对地面成像,而ISAR则固定在地面对非合作目标进行成像,其成像方式如图1所示。
图1(a)为机载SAR工作模式,波束始终指向同一成像区域来获得该区域场景的高分辨率图像(合成孔径越大分辨率越高)。将机载直线飞行造成的雷达与照射区域之间的距离变化进行补偿后,SAR可看作飞机绕雷达做圆周运动,如图1(b)所示。等效于雷达跟踪不同目标旋转,这就是一般ISAR的工作模式[2]。

通过以上分析可知,在运动补偿最理想的情况下,目标相对于雷达的平动分量不存在,而只有转动分量,则对目标成像相当于把目标移动到转台上,对转台上的转动目标进行成像,这就是经典的转台成像。
因此,为使ISAR高质量对目标成像,运动补偿是其关键技术,其中包括包络对齐和相位校正两部分。而包络对齐为后续校正和成像的基础。在距离向将目标回波对准后,方位向补偿以及其他散焦问题将成为考虑的重点[3]。由此可见包络对齐在ISAR中占有重要地位,本文着重研究包络对齐的一种新迭代方法。
2 包络对齐
如前所述,当雷达工作在高频区间时,根据雷达目标的散射点模型,若干离散的散射点可被近似看成构成雷达目标的基本单元,依此可知,此时经目标反射的雷达回波可被认为发射脉冲经过各散射点后向散射形成的各脉冲回波的向量和。相对来说,逆合成孔径雷达在成像期间目标的转角非常小,大概只有2°~3°,所以可以认为目标的反射系数和散射点相对位置基本不变。然而,视角的微小变化,会使散射点相对于雷达的距离发生变化,各个距离单元的回波幅度也会随视角的变化而变化。因此描述目标散射点模型和回波序列关系成为包络对齐的基础。
2.1 散射点模型和回波序列
当对两个波形相同而起点不同的信号作对齐处理时,可采用不同的延迟计算两者之间的相关系数。当相关系数最大时,两波形会完全重合,此时对齐是最准确的。然而,这种方法只是针对相邻两次对齐的情况,在实际成像中,所需要几百个甚至更多的序列,即需要进行更多的相邻相关对齐[4]。此时这种方法就不太实用,其误差很小,但会发生误差积累效应从而产生包络漂移;同时若在回波序列中有个别瞬时波形存在特异变化,则该处的包络对齐会产生很大的误差,相邻相关后会发生包络突跳,这些误差会使后期成像变得非常差。为定量地研究这些误差,首先讨论基本的回波序列和目标散射点模型的关系[5]。

从上式中看到,在一定的散射点分布模型下,|sn(m)|2由自身项和交叉项两部分组成。由于在小的观测角范围内目标散射点的强度|?滓n,k|是不变的,而散射点的时延rn,k(m)所引起的散射点位置变化很小,所以自身项为不随m变化的稳定项。但交叉项中,相位?兹n,k,l(m)随观测序号m变化较快,使得交叉项为随m变化较快的起伏项。对于目前宽带雷达的距离分辨率,多数距离分辨单元内包含的散射点个数在10的数量级上,因而多数距离单元的|sn(m)|2有一定的稳定值,同时也随观测序号m有一定的起伏[6]。
若在目标相对于雷达的散射点模型基本不变的转角范围内,将式(2)对m求平均,则由于信号的自身项不变,而交叉项互相抵消,当积累次数很多时,交叉项就会减得很小,因此得到的平均功率像基本为其自身项:
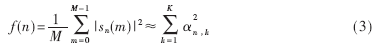
上式说明,只要不考虑各距离单元间散射点的迁移,各次观测时间的平均功率像近似为散射点强度在径向的标量和[7-9]。因此,如果对观测期间各次回波的功率像求平均,可得到一较稳定的平均功率像,其开方即为平均距离像。
此处所得到的平均距离像同时也是后续迭代计算的标准。
2.2 迭代相关对齐法
经过上面的分析可以看出,各次回波距离像包含了两项内容,即散射点的交叉项和自身项。各次回波之间的相关性受回波包络幅度的起伏影响,而这一影响正是由交叉项引起的。但是可以采用在包络对齐之后,对各次回波包络求平均值的方法使得交叉项互相抵消,使平均距离像受到的影响几乎可以忽略,从而使平均距离像与各次回波都有较强的相关性。如果采用平均距离像作为参考包络对各次回波作相关对齐会得到较好结果。
此种方法是在包络对齐之后进行的,而在包络对齐之前无法得到好的平均距离像,因此只能采用其他方法。本文针对上述几种情况提出了迭代相关法,对这一问题进行了很好的解决。
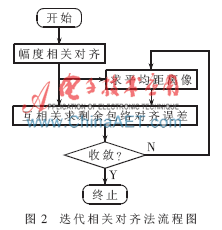
(1)采用相邻幅度相关法等一般方法进行一次包络对齐,并将包络对齐后的距离像进行求平均得到一次平均距离像[10]。此时得到的平均距离像会比较差,因为可能存在漂移和突跳误差。
(2)用得到的这一比较差的平均距离像与各次回波距离像作相关处理,进一步以相关系数最大为标准进行相关补偿剩余包络对齐误差。可进一步对对齐后的距离像求平均,消除前面得到的平均距离像本身的较大误差,得到一新的平均距离像估计,并继续用这一平均距离像来校正各次回波的包络对齐误差。
对上述过程进行迭代,直至收敛,这一过程称为迭代相关对齐法。实际表明一般4~6次即可收敛。其流程图如图2所示。
3 仿真结果对比
从以上分析可以看出,为了有效消除交叉项的影响,应该取时间间隔较大的功率像求平均,平均距离像是各次回波的包络平均。本文使用仿真模拟,生成256次回波,每次回波中的散射点间有微小时延,且振幅不变。现以不同数目的等间隔回波作平均得到平均距离像,仿真结果如图3所示。
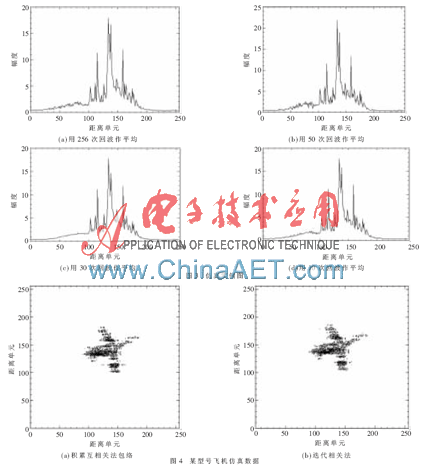
其中,图3(a)使用全部的256次回波作平均,图3(b)、图3(c)、图3(d)分别采用50次、30次和10次回波,可以看出几乎没有差别,说明稳定的平均距离像只需采用10次回波作平均就可以得到了。因此大大缩减了运算时间。 在此基础上,继续使用仿真数据对某型号飞机进行处理和分析,如图4所示。
可以看出,原方法即积累互相关法包络和迭代相关法均未发生包络漂移和突跳的情况,而积累互相关方法在对目标主体的对准方面并没有迭代法积累效果明显,成像清晰度也较迭代法逊色。
本文首先介绍了ISAR雷达的工作原理,并阐述了包络对齐对成像效果的重要影响。从散射点模型出发,分析了距离像相关性,使用距离平均像概念推导出迭代相关法。其中距离平均像与所有的距离像有很强的相关性,因此可以将它作为相关模板进行对齐。最后通过仿真数据选择出计算平均距离像所需回波次数,同时与积累互相关法进行对比,可以看出迭代相关法对成像效果有明显改善。
参考文献
[1] 左衍琴.频率步进雷达高速目标成像中的运动补偿方法研究[D].长沙:国防科技大学,2009.
[2] 吴瑾.关于合成孔径激光雷达成像研究[J].雷达学报,2012,1(4):353-360.
[3] 保铮,刑孟道,王彤.雷达成像技术[M].北京:电子工业出版社,2005.
[4] 高磊,黄小红,陈曾平.基于包络相关法的包络对齐方法改进[J].雷达科学与技术,2007,5(3):53-56.
[5] 刘永坦.雷达成像技术[M].哈尔滨:哈尔滨工业大学出版社,2003.
[6] 李燕平.单/双基SAR成像和运动补偿研究[D].西安:西安电子科技大学,2008.
[7] 韩兴斌,胡卫东,郁文贤,等.一种复杂运动目标的ISAR成像算法[J].电子学报,2007,35(6):153-158.
[8] 高建军.多径和海杂波干扰下的舰船ISAR成像及横向定标[D].哈尔滨:哈尔滨工业大学,2009.
[9] 叶旭.舰船目标ISAR成像研究[D].南京:南京航空航天大学,2008.
[10] 陈安.逆合成孔径雷达成像问题研究[D].南京:南京理工大学,2004.