0 引言
工业机器人已经成为先进制造业的支撑技术，在焊接、切割、搬运、喷涂等工业领域得到了广泛的应用，成为衡量一个国家制造业水平的重要标志[1]。机器人的出现是为了适应制造业规模化生产、解决单调重复的体力劳动和提高生产质量，因此从一诞生就掀起了全球研发和应用的热潮[2]，并逐渐成为柔性制造系统、自动化工厂和计算机集成制造系统中不可缺少的自动化单元[3]。
机器人控制的常用算法有 PID 控制、自适应控制、鲁棒控制、迭代学习控制、滑模变结构控制、反演控制设计方案、神经网络控制和模糊控制等[4]。随着计算机技术和智能控制理论的发展，先进的智能 PID 控制策略相继被提出，为复杂动态不确定机器人系统的控制提供了新的途径[5]。例如，任国华等学者提出了一种“多项式PD控制+机器人全局位置重力补偿”的控制策略，并通过Lyapunov直接法证明了闭环系统的全局稳定性；另外由于增益的调整可能导致电机的力矩饱和，从而影响控制性能，甚至导致系统不稳定，基于此，又给出了简单的增益调整规则[6]。胡克满等人提出了一种基于BP神经网络的自适应PID控制策略实现了六自由度喷涂机器人的位置控制，通过BP神经网络的学习和在线辨识，自适应地调整PID的控制参数，从而获得较好的控制性能和应对参数变化的鲁棒性[7]。昝鹏等人针对由空气压橡胶驱动器驱动的三自由度微型机器人，提出了基于BP神经网络PID控制策略，用系统输出的预测值来代替实测值, 实时计算权系数的修正量来改变控制参数以提高控制效果，该方法弥补了传统PID控制方法的不足[8]。
本文针对传统PID控制算法在串联机器人的轨迹跟踪控制中存在的问题，提出了一种基于改进PID控制算法的串联机器人轨迹跟踪控制策略，采用自适应学习策略对PID控制算法进行优化，以减小原算法的控制误差。
1 PID控制算法
PID控制是较早流行起来的控制方法之一，由于其在鲁棒性上具有较好的性能，被大量作用于过程的控制中，并且使用也比较简便，可靠性较高。
模拟PID调节器框图如图1所示。
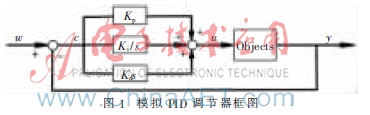
常规控制器作为一种线形控制器，其数学模型为：
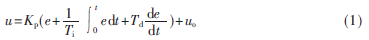
其传递函数为：
其中：Kp为一个特定的比例系数，Ti为一个代表积分时间的常数，Td为一个代表微分时间的常数，e为调节器的输入偏差数值，uo是控制量的基准。
积分环节的功能是消除静差，但容易造成超调和振荡。比例环节的功能是能快速找出误差，却无法去除稳态误差，并且因为过大的作用容易引发不稳定。微分环节的功能是优化系统的动态特性，通过减小超调等来降低振荡，并能够加强其稳定性。
2 基于改进RBF神经网络的PID控制算法
2.1 基于减聚类优化的RBF神经网络
RBF神经网络的结构如图2所示。
设RBF神经网络输入节点个数为n，隐含层节点个数为m，输出节点个数为p，则第j个隐含层节点的输出为：
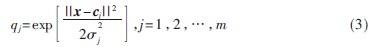
其中，x为输入向量，cj为中心矢量，j为基宽带参数，并且有：
网络输出层第k个节点的输出如式(5)所示：
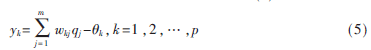
其中，wkj为 qj→yk的权值，k为阈值。
选取以下函数作为网络训练的目标函数：
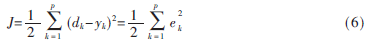
其中，dk为理想输出， yk为实际输出。
针对传统RBF神经网络隐含层单元数目难确定的问题，本文首先采用减聚类的方法对隐含层中心数目进行优化。设一个立体的 n维空间 p个数据点(x1，x2，…，xp)，根据下式设定数据点xi处的密度指标：
然后对上式求出的密度指标Di进行最大值的选取，选取结果为聚类中心，记为xc1，接着对上述密度指标进行更新操作，如下式所示。
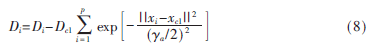
对更新后的密度指标，重复最大值选取操作，设定聚类中心，直到满足下式要求时，结束循环。
接着，采用Logistic映射对RBF神经网络进行优化。Logistic映射的变量转换，如下式所示。
将其代入Logistic映射中，得到：
xn+1=1-2(xn)2(11)
最后，采用减聚类的方法和改进的Logistic映射对RBF神经网络进行优化，具体步骤如下：
(1)采用减聚类的方法得到RBF神经网络的聚类数目，记为k，将输入样本记为Xi；
(2)对聚类中心进行随机选取，并对其到输入样本的距离进行计算。
其中，i表示聚类中心，并且有i=1，2，…，k；j表示输入样本，并且有j=1，2，…，N。
(3)对式(12)得到的到输入样本的距离di进行求平均操作，如下式所示。
(4)采用Logistic对中心值进行精度的提升，如下式所示。
其中，Yn的取值范围为(-1，1)。
(5)在迭代n次后，得到最终的聚类中心，如下式所示。
c(n)t=c(n-1)t+zn Yn-1(15)
其中，zn=z0 exp(·n)为迭代中的变化参数。
(6)循环n次迭代，比较聚类中心的大小，选取其中的最小值，作为RBF神经网络聚类中心。
2.2 基于改进RBF神经网络的PID控制算法
针对串联机器人系统的控制需求，本文采用上文提出的改进RBF神经网络对传统PID控制算法进行改进，以达到更精确的串联机器人轨迹跟踪控制。控制策略如图3所示。
图3中的r(t)为给定信号，y(t)为机器人支路的输出信号，则基于改进RBF神经网络的PID控制误差为：
error(k)=r(k)-y(k)(16)
PID控制算法的各项参数分别为：
x(1)=error(k)-error(k-1)(17)
x(2)=error(k)(18)
x(3)=error(k)-2error(k-1)+error(k-2)(19)
将式(17)~(19)代入增量式PID控制算法中，则控制算法为：
u(k)=u(k-1)+kp x(1)+ki x(2)+kd x(3)(20)
神经网络的训练指标为：
代入到增量PID控制器的参数kp、ki、kd的表达式为：
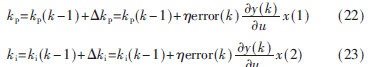
式中，![N1Q0X$]1N3QI5MCBT)~A2)3.jpg](http://files.chinaaet.com/images/2015/08/14/6357518767081100003032266.jpg "N1Q0X$]1N3QI5MCBT)~A2)3.jpg")
为学习速率，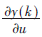
为串联机器人各条支路的输出对支路控制的灵敏度信息，其表达式为：
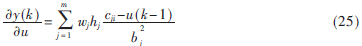
3 算法性能仿真
为了验证本文提出的改进算法的有效性，对其进行仿真实验，并与传统算法进行对比。串联机器人额定功率为400 W，额定转速为3 000 r/min，额定转矩为1.3 N·m，最大转矩为0.67 N·m，某两次位移控制的结果如表1所示，多次实验的对比结果如图4～图6所示。
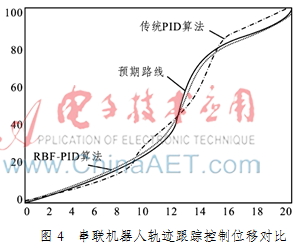
从仿真结果中可以看出，本文提出的改进PID控制算法因为通过改进RBF神经网络的自适应学习和调整，其对串联机器人的位移控制与预期位移近似，其控制的平均误差可以达到3%以内，并且其平均响应时间为1 s，远远小于传统PID算法。
综上所述，本文提出的改进算法比传统PID控制算法对串联机器人轨迹跟踪控制的效果要好，大大降低了其误差，提高了PID控制器的鲁棒性。
4 结论
串联机器人系统是很复杂的非线性系统，其轨迹跟踪控制是在串联机器人控制问题中的一个重要方面。本文提出了基于改进PID控制算法的串联机器人轨迹跟踪控制策略，从仿真结果中可以看出，本文提出的改进算法的误差远远小于传统PID控制算法的控制误差，证明该控制策略切实有效。
参考文献
[1] 朱大昌，刘运鸿.3-RPC型并联机器人模糊PID控制系统研究[J].机械传动，2014，38(2)：114-117.
[2] 李楠，李文鑫.改进的关节机器人神经网络PID控制器[J].控制工程，2013，20(6)：1052-1054.
[3] 刘国荣，张扬名.移动机器人轨迹跟踪的模糊PID-P型迭代学习控制[J].电子学报，2013，41(8)：1536-1541.
[4] 丁度坤，谢存禧.高速运动机器人关节神经网络PID自适应控制研究[J].制造业自动化，2013，35(21)：18-20.
[5] 张超，王琦，姚永刚.基于AC-PID控制器的焊接机器人仿真[J].焊接技术，2013(7)：58-62.
[6] 任国华.移动机器人轨迹跟踪与运动控制[J].机械设计与制造，2014(3)：100-102.
[7] 胡克满.基于改进型PID控制算法在小型仓储物流智能机器人中的应用研究[J].物流技术，2012(4)：24-27.
[8] 昝鹏，颜国正，于莲芝.基于自适应模糊PID控制的气动微型机器人系统[J].仪器仪表学报，2007，28(9)：1543-1547.
[9] Wei Xianming.Study and simulation of intelligent control methods based robot walking on water[J].Journal of SystemSimulation，2014，26(1)：163-168.
[10] 吴孔逸，霍伟.不确定移动机器人编队间接自适应模糊动力学控制[J].控制与决策，2010(12)：1769-1774.
[11] 张琨.基于自适应RBF网络补偿的智能车辆循迹控制[J].控制与决策，2014，29(4)：627-631.
[12] 申铁龙.现代控制系统设计方法与倒立摆控制问题[J].控制理论与应用，2004，21(5)：728-728.
[13] Cao Yuli.Research on two-wheeled self-balanced robotbased on variable universe fuzzy PID control[J].2013，30(2)：347-350.
