
李俊,周薇娜
(上海海事大学 信息工程学院,上海 201306)
摘要:为了实现快速运动目标检测,利用低秩矩阵恢复原理进行视频前景检测,主要针对低秩矩阵恢复算法存在的耗费大部分运算时间且运算较为复杂的奇异值分解问题,应用统一计算结构装置(CUDA)第三方库实现加速计算奇异值分解的低秩矩阵恢复算法优化,得到快速且高效的前景检测方法。基于开源视频序列实验,与原有的低秩矩阵恢复算法进行各项参数的比较,其中加速倍数达一倍以上。实验结果证明,经过优化的算法运算时间变短,具有更高效率。
关键词:低秩矩阵恢复;前景检测;统一计算结构装置
0引言
目标检测是把视频序列中感兴趣的目标分割出来,作为许多视觉应用中最基础的部分,深入探讨其相关算法研究以提高其检测性能与精度,显得相当重要。传统目标检测算法计算较为复杂,检测精度相对较低,性能也较低下。随着计算机技术的高速发展,所拍摄的视频序列图像分辨率也越来越高,这使得视频序列中图像数据量过大和数据维数过高,增加目标检测计算难度。对高维数据降维,用降维得到的低维数据表征原有的高维数据从而降低数据计算复杂度成了视频图像数据处理的重要方法。主成分分析(Principal Component Analysis,PCA)是一种很有效的分析高维数据的工具,把高维数据投影到低维空间,奇异值分解(Singular Value Decomposition,SVD)使得PCA有了稳定高效的计算能力,但当矩阵元素受到严重破坏时,PCA则对矩阵估计不准确。为了改善PCA对这种情况的处理,CANDES E J提出了鲁棒主成分分析[1](Robust Principle Component Analysis,RPCA),也称低秩矩阵恢复[2],指元素受到严重破坏的矩阵也得以恢复。
一般说来由视频数据构造成的观测矩阵可以分解为稀疏和低秩两个矩阵,矩阵恢复时可以用凸优化的方法,视频前景检测拟合这种分解特性。前景检测是从拍摄的视频中分离出背景和前景,由于视频的背景基本是不变的,因此如果把每帧当做矩阵的各列,那么此矩阵将是低秩的,低秩矩阵恢复可以同时完成背景和前景分离,得到的前景即为需要检测的目标。
低秩矩阵恢复算法运行在MATLAB平台上,MATLAB虽易用性强,但是有着计算慢、效率低等缺点。经过对算法和CUDA[3]深入分析,使用MATLAB和C++ 的MEX混合编程,进行了在MATLAB内调用CUDA第三方库加速原有算法的运算,经加速优化后,低秩矩阵恢复前景检测方法效率更高。最后基于真实数据实验,进行经过优化后的算法与原算法各项参数的比较。
1低秩矩阵恢复
观测得到的数据组成的数据矩阵D秩一般很低,为了恢复它的低秩结构,把矩阵D分解成一个低秩矩阵和一个稀疏矩阵的和,即D=A+E,A未知是低秩的,E也未知是稀疏的。当矩阵E的元素服从独立同分布的高斯分布时,PCA可解SVD得到最优的矩阵A,即求解下面的最优化问题:
min∫‖E‖Fs.trank(A)≤c,D=A+E (1)
其中,‖.‖F为F范数,c为子空间维数。当E不理想时,经典PCA对A的估计就相当不准,WRIGHT J 等人提出的RPCA很好地解决了上述问题。
同PCA一样,RPCA的问题可描述为:观察数据矩阵D为已知,D=A+E,A、E未知,A为低秩的,但是E稀疏且非零元素E可能无限大,要从中恢复出A,需得到观察数据D的最小的秩,且干扰误差是稀疏的。通过以下优化问题来描述:
minA,Erank(A)+λE0s.tA+E=D(2)
其中,rank(A)为A的秩;.0为求解零范数,表示矩阵中不为零元素数目;λ为正常数。因为没有有效方法解决这个NPHard问题,所以决定对式(2)做松弛变化转换成容易求解的凸优化问题,将l0范数由l1范数替代,用核范数A=∑iσi(A)代替A的秩,即:
minA,EA*+λE1s.tA+E=D(3)
该问题也被称之为主成分追踪(Principal Component Pursuit,PCP),在一定条件下,求解式(3)可以得到理想且唯一的A和E。将以上的凸优化问题称为RPCA,该方程式在实际应用中性能良好,能从高达1/3严重腐蚀的观测值中恢复真实的低秩矩阵,并且具有优秀的理论保证。例如,对一般的矩阵A,它可以显示成功纠正错误恒比,甚至当 A 的秩是近似地正比于环境度:rank(A)=Cm/log(m)。参考文献[1]也给出了结论定理:如果A0为n×n矩阵,其秩rank(A0)≤ρrnμ-1·(logn)-2,E0是随机稀疏的n×n矩阵,基数m≤ρsn2ρrρs,其中ρr为低秩率,ρs为稀疏率,当λ=1/n时,PCP能够准确恢复出L∧=L0,S∧=S0的概率为1-O(n-10)。对于任意矩形矩阵,对λ=1/max(m,n)有与上相同的结论。
2算法
前景检测是把目标由视频里提取出来。因为视频的背景基本是不变的,假设视频有n帧图像,把每帧当做矩阵D每一列,由每帧图像的像素构成的m维列向量作为矩阵D每一行,得到大小为m×n低秩矩阵D,因此可用低秩矩阵恢复来恢复出背景。低秩矩阵A可作为视频中有很大相关性的背景部分,稀疏矩阵E则可作为分布稀疏的前景部分也即感兴趣的目标。
有许多方法可求解RPCA问题[47],本文对非精确增广拉格朗日乘子法(IALM)中的奇异值分解计算进行加速优化,使得能够加速计算奇异值分解,算法运算效率提升,运行时间缩减。
构造增广拉格朗日函数:
L(A,E,Y,μ)=‖A‖+λ‖E‖1,1+
<Y,D-A-E>+μ‖D-A-E‖2F/2(4)
其中,Y∈Rm×n为约束乘子,μ>0为惩罚参数,·表示计算内积,‖·‖F表示F范数。每一步最小化式(4)时使用轮流更新的方法,先保持Y与E不变,求得使L最小的A,然后保持Y与A不变,求使L最小的E,这样迭代次数就可收敛到这个子问题的最优解。更新A时:
arg minAλ‖A‖* + μ2‖D-A-E + μ-1Y‖2F
=Θμ-1 (D-E + μ-1Y)(5)
更新E时:
arg minEλ‖E‖1 + μ2‖D-A-E + μ-1Y‖2F
= Λμ-1 (D-A + μ-1Y)(6)
轮流更新,直到对子问题求解收敛时为止,该算法被称为精确增广拉格朗日乘子法(EALM),见算法1[4,8]。
算法1
(1)初始化Y0,E0=0,μ0,k=0
(2)while not converged do
(3)E0k+1=E*k,j=0
(4)while not converged do
(5)(U,S,V)=svd(D-Ejk+1+μ-1kY*k)
(6)Aj+1k+1=UΛμ-1k[S]VT
(7)Ej+1k+1=Λλμ-1k[D-Aj+1k+1+μ-1kYk]
(8)j=j+1
(9)end while
(10)Y*k+1=Yk+μk(D-A*k+1-E*k+1),μk+1=ρμk
(11)k=k+1
(12)end while
称算法1为精确增广拉格朗日乘子法,原因在于最外层的循环并不需要求出子问题的精确解,事实上,只要将A和E都更新一次得子问题的一个近似解,这样得到的最优解就可使算法收敛到原问题,因此可以得到简洁且收敛更快的算法——IALM,见算法2[4,8]。
算法2
(1)初始化Y0,E0,μ0,k=0
(2)while not converged do
(3)(U,S,V)=svd(D-Ek+μ-1kYk)
(4)Ak+1=UΛμ-1k[S]VT
(5)Ek+1=Λλμ-1k[D-Ak+1+μ-1kYk]
(6)Yk+1=Yk+μk(D-Ak+1-Ek+1)
(7)更新μk
(8)k=k+1
(9)end while
以上算法会耗费大量时间计算奇异值分解,所以找到快速处理奇异值分解计算的方法,对于整个算法的执行效率将会大有改善。本文基于CUDA 架构第三方CULA[9 10]库在MATLAB中实现加速优化算法中奇异值分解的计算。MATLAB中CUDA加速的原理为:CPU执行流程控制的操作代码,一些需要并行运算的操作代码放在GPU中处理,这样算法运算时间将大幅度减少。CUDA计算的流程如图1所示。

经过仔细阅读CULA参考手册和CULA编程指南,分析低秩矩阵恢复算法,编写可以在MATLAB里面通过一些接口使用CULA库加速的culaSvd mex源文件。首先,需要在MATLAB 里面处理多种CULA的数据类型,MATLAB和CULA 支持的4个主要的数据类型为: 单精度实数、双精度实数、单精度复数和双精度复数。由于MATLAB MEX编译器与CULA 支持C++语言,可以通过代码来实现数据类型的处理,用C++模板来处理所有的4个MATLAB数据类型,使用MATLAB函数mxGetClassID() 和 mxIsComplex()确定输入矩阵的精度和复杂度。上述代码主要包括3个部分,SVD函数的CULA头文件和MATLAB数据类型和接口的头文件、支持4种MATLAB数据类型的模板函数、在MATLAB中调用的C++模板所需要的网关函数。其次,因为CULA和 MATLAB以不同的类型存储复杂的数据,创建helper函数,实现两个类型之间的转换。 创建好helper函数后,通过查阅CULA的xGESVD函数的文档可以发现,MATLAB中对角阵返回奇异值,而CULA返回一个向量,MATLAB返回V,而CULA返回V的转置,为了对接 MATLAB 的接口,必须从奇异值向量转换成一个对角矩阵并转置。至此完成了culaSvd程序,在MATLAB中用MEX命令编译culaSvd.cpp源文件生成二进制mex文件,完成MATLAB中实现在底层调用经CULA 加速优化后的奇异值分解。
3实验结果及分析
本节将原有算法与基于CUDA优化后的算法进行运行效果比较,测试是基于拍摄的真实数据进行的,试验运行环境配置为:Intel Core i5 M 520 2.40 GHz CPU,4 GB 内存,Nvidia 公司的GT218 GPU,编程环境为MATLAB R2010a+Visual Studio 2010+CUDA Toolkit Version 4.0+CULA R12,选取的视频是拍摄的学校路口某个时刻的场景。视频序列总共为200帧,每帧大小为576 768,由此组成的观测矩阵为M(27 648×200)。

图2为选取的第150帧3种算法运行效果对比图。表1为取150帧进行前景检测,两种算法及其加速改进后算法的运算时间、迭代次数、SVD时间及SVD次数的比较。图2第180帧3种算法仿真对比图

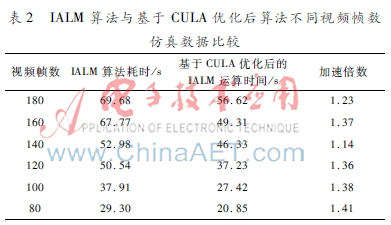
表2为分别取180帧、160帧、140帧、120帧、100帧和80帧进行前景检测,为了得到精确运行时间,分别进行100次运算,然后取平均运行时间,计算算法的运行时间、平均加速倍数。对视频进行处理,将其裁剪为不同分辨率的视频,对其进行测试,表3 为分别采用不同分辨率进行视频测试时两种算法的运行时间及其加速倍数。
从仿真效果可以看出,经CULA优化后的算法分离出的背景A3比其他两种原有的算法得到的背景A1和背景A2相比,前景目标更加分明,前景目标检测效果更好。

表1表明,优化改进后的算法运行效率有所提升。表2取不同的视频帧数进行前景目标检测,表明实现了至少1倍以上加速比。最后表3给出了不同测试视频的运行结果,表明随着图像尺寸的加大,加速比增大。综合得知,本文的优化改进算法效率更高。
4结论
本文应用CULA加速优化后的低秩矩阵恢复算法实现前景目标检测,加速优化后的算法与原有算法相比,奇异值分解次数减少,表明算法里的奇异值分解计算得到加速改进,因此算法的运行时间得以较大幅度缩短。仿真结果表明,本文加速优化后的算法有更好的前景目标检测效率。本文的前景目标检测算法在计算效率上得到改善,发挥了软硬件结合的效果,这种学习成本低廉、使用代价较小、运行效率较高的优点弥补了MATLAB计算速度上的缺点,也使得视觉应用的研究有了良好的开端。
参考文献
[1] CANDES E J, Li Xiaodong, Ma Yi, et al. Robust principalcomponent analysis[J]. Journal of the ACM,2009,58(3):233279.
[2] WRIGHT J,GANESH A,RAO S,et al.Robust principal component analysis:exact recovery of corrupted low rank matrices via convex optimization[C].Proceedings of Neural Information Processing Systems (NIPS), 2009,87(4):20:320:56.
[3] NVIDIA Corporation. NVIDIA CUDA programming guide[Z]. 2009.
[4] Lin Zhouchen,Chen Minming,Ma Yi.The augmented Lagrange multiplier method for exact recovery of a corrupted lowrank matrix[R]. Eprint Arxiv,2010.
[5] GANESH A, Lin Zhouchen, WRIGHT J, et al. Fast algorithms for recovering a corrupted low rank matrix[C].International Workshop on Computational Advances in MultiSensor Adaptive Processing,2009:213216.
[6] Lin Zhouchen, GANESH A,WRIGHT J,et al.Fast convex optimization algorithms for exact recovery of a corrupted low rank matrix[C].Proceedings of Computational Advances in MultiSensor Adaptive Processing (CAMSAP),2009.
[7] YUAN X, YANG J. Sparse and low rank matrix decomposition via alternating direction methods[R].Hong Kong: Hong Kong Baptist University,2009.
[8] Chen Minming.Algorithms and implementations of matrix reconstruction [D] . Beijing: Graduate School Chinese Academy of Science,2010.
[9] EM Photonics Corporation. CULA reference guide[Z]. 2014.
[10] EM Photonics Corporation. CULA programmers guide[Z]. 2014.