0 引言
我国现役飞机中，直流电源系统占有重要的地位。该电源系统中对过压保护电路的延时特性有特殊要求，即反延时特性，电源过压值越高，延时保护时间越短。为满足反延时特性的要求，参考文献[1]提出了通过延时电路并联的实现方法，根据反延时的要求确定并联的支路数目，由此得到一种反延时电路。
过压保护电路是直流电源系统安全运行的保障。针对其反延时特性提出的反延时电路的可靠性分析是必要的。电路中电子元器件的寿命服从指数分布[2]。对于指数分布，在定时、定数截尾数据无缺失的情形下，理论和具体的应用方法均比较成熟。曹晋华，程侃[3]的《可靠性数学引论》对无数据缺场合进行了全面的总结。真实试验环境下，试验机理、观测手段及记录手段不当等会导致部分样本的丢失，在不能再次进行试验的情形下，对不完全样本的可靠性分析，具有一定的研究价值。在定数截尾有缺失的情形下，参考文献[4]给出了单、双参数指数分布中参数的最佳线性无偏估计及近似极大似然估计；参考文献[5]给出了指数分布基于定数截尾有缺失样本的Bayes估计，并给出了一种近似算法，但计算稍有复杂。参考文献[6]结合参数的最佳线性无偏估计导出了单参数指数分布的Bayes估计。
对于参考文献[1]中的反延时电路，参考文献[7]在定时无替换数据无缺失的情形下，给出了可靠性指标的Bayes估计及极大似然估计。鉴于真实的试验环境，本文结合参数的最佳线性无偏估计，在定数截尾数据缺失的情形下，给出反延时电路可靠性指标的Bayes估计，并结合矩估计法给出了超参数的估计。
1 系统可靠性指标
反延时电路中每个电子元器件的寿命均服从参数为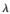
的指数分布，其概率密度函数为：
反延时电路图在参考文献[1，7]中已给出，参考文献[7]给出了对应的可靠性工程图，如图1所示。
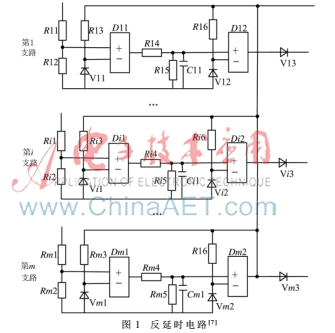
选取反延时电路系统中单个电子元器件的失效率r(t)、系统可靠度Rs(t)及平均寿命MTTFs作为可靠性指标。由参考文献[7]可知，当有m种延时要求时，单个部件失效率[7]：
![B]WZ30J688%S~E]KH}7IZCY.png](http://files.chinaaet.com/images/2017/01/25/6362096395426500001461524.png "B]WZ30J688%S~E]KH}7IZCY.png")
2 Bayes估计
在定数截尾数据有缺失的情形下讨论可靠性指标的Bayes估计。随机抽取n个反延时电路系统中的电子元器件进行试验。当电子元器件的失效数达到r时便停止试验。得到的失效时刻依次为0≤t1≤t2≤…≤tr(r≤n)，但最终只获得了k(k<r)个观察值，由参考文献[5]可知t的似然函数形式复杂，求解可靠性指标的Bayes估计十分困难，为此本文采用参考文献[6]中基于最佳线性无偏估计的近似方法来求得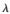
的后验密度函数。
2.1 基于最佳线性无偏估计的后验密度函数
已知t1，t2，…，tr独立同分布，且服从分布F(t|)=1-exp(-t)，t≥0，令t0≡0，则0≡t0≤t1≤t2…≤tr为其顺序统计量。设：
Mj=(n-j+1)(tj-tj-1)(5)
对(5)变形可得：
由此可知指数分布的顺序统计量可以表示成：
由参考文献[3]可知，M1，…，Mr独立同分布t≥0，则：
其中r0=0，i=1，2，…，k，且由上述条件可知X1，X2，…，Xk是相互独立的，从而利用参考文献[8]中Gauss-Markov定理可以得到的最佳线性无偏估计(BLUE)为：
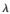的先验分布为伽马分布，即：
![{B}{I`J_TJ2`U53[7WU9X]T.png](http://files.chinaaet.com/images/2017/01/25/6362096409576300009862618.png "{B}{I`J_TJ2`U53[7WU9X]T.png")
则
的后验分布为：
2.2 可靠性指标的Bayes估计
单个电子元器件的失效率在平方损失下的Bayes估计为：
![QV9W7V7LZA2V5B]]$FWF7F8.png](http://files.chinaaet.com/images/2017/01/25/6362096414933700006892359.png "QV9W7V7LZA2V5B]]$FWF7F8.png")
系统的可靠度为：
上式展开后每一项均可表示为Ae-Bt，A、B为常数，即
，当m给定，Ai，Bi均是已知的常数。因此令P(A，B)=Ae-B?姿t，则P(A，B)在平方损失下的Bayes估计为：
![5C~KEHY9QNG)F]M6P_PFRKD.png](http://files.chinaaet.com/images/2017/01/25/6362096417734500003344979.png "5C~KEHY9QNG)F]M6P_PFRKD.png")
则系统的可靠度Rs(t)在平方损失下的Bayes估计为：
对应的系统平均寿命的近似Bayes估计为：
当m给定后便可计算出Ai和Bi，带入式(22)、(23)，便可以得到系统可靠度及平均寿命的Bayes估计。
2.3 超参数估计
式(19)、(22)、(23)中均含有未知参数![UW~S]3(1`EN%D{OU]OL6T1S.jpg](http://files.chinaaet.com/images/2017/01/25/6362096427161600006685921.jpg "UW~S]3(1`EN%D{OU]OL6T1S.jpg")
，即超参数，则3个可靠性指标的Bayes估计不能直接应用。丢失数据的个数要远小于样本总量，因此在有数据缺失的情况下，通过矩估计法来近似估计超参数![UW~S]3(1`EN%D{OU]OL6T1S.jpg](http://files.chinaaet.com/images/2017/01/25/6362096427881900006923580.jpg "UW~S]3(1`EN%D{OU]OL6T1S.jpg")
。先计算t的一阶矩和二阶矩：
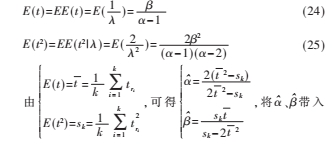
带入式(19)、(22)、(23)中，得到可靠性指标的Bayes估计。
3 数值模拟
为观察本文方法的估计效果，针对并联6个支路的反延时电路系统，将可靠性指标的Bayes估计与应用参考文献[4]方法所得的极大似然估计（MLE）进行了数值模拟比较。根据GB/T1772[2]中规定的电子元器件失效率等级标准，在模拟中，取
的真值为
=2×10-5(1/h)，对应的系统可靠度Rs(24 000h)为0.668 4。取n=30，70两种情况，k为数据缺失个数，r为失效数。为排除偶然因素的影响，对于每种组合随机模拟10 000次，并取所得估计值的均值作为最终的估计结果。
利用蒙特卡罗方法模拟产生服从指数分布的样本数据，再依据k，r的取值，得到最终的截尾样本数据。根据2.2、2.3节所得结果计算出可靠性指标的Bayes估计，如表1、表2所示，相对偏差对比如图2所示。
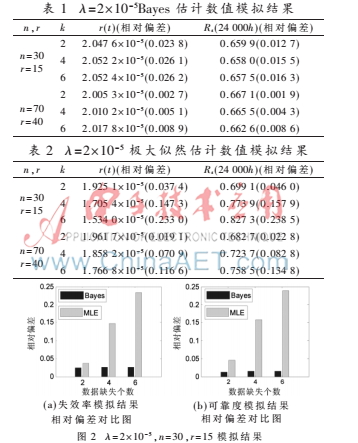
结合上述图表可以看出：(1)单个电子元器件的失效率及系统的可靠度的Bayes估计的相对偏差均小于MLE的相对偏差，可见Bayes估计的估计精度要高于MLE；(2)当截尾样本数据容量一定时，随着数据缺失个数k增加，单个电子元器件的失效率及系统的可靠度的Bayes估计和MLE的相对偏差逐渐增大，估计精度降低；且k对MLE的影响大于Bayes估计；(3)r增加时，电子元器件的失效率及系统的可靠度的Bayes估计和MLE的相对偏差逐渐减小，估计精度升高。
通过对比发现，Bayes估计的估计效果要优于MLE。这是因为Bayes估计结合了有效的先验信息，且受数据缺失个数的影响要小于MLE。
4 结论
本文讨论了定数截尾数据缺失的情形下，反延时电路可靠性指标的Bayes估计。通过数值模拟，将Bayes估计与相应的MLE进行了分析对比。结果表明Bayes估计的相对偏差均要小于所对应的MLE的相对偏差，且受数据缺失个数的影响要小于MLE。所以在定数截尾数据有缺失的场合下，对反延时电路系统的可靠性指标进行估计时，可选用Bayes估计，并且在真实的试验环境下，应避免数据的大量缺失。
参考文献
[1] 张益平.飞机低压直流电源系统研究[D].西安：西北工业大学，2004.
[2] 付桂翠，陈颖，张素娟，等.电子元器件可靠性技术教程[M].北京：北京航空航天大学出版社，2010.
[3] 曹晋华，程侃.可靠性数学引论(修订版)[M].北京：高等教育出版社，2012.
[4] BALASUBRAMANIAN K，BALAKRISHNAN N.Estimationfor one-and two-parameter exponential distributions undermultiple type-II censoring[J].Statistical Papers，1992，33(1)：203-216.
[5] 王乃生，王玲玲.定数截尾数据缺失场合下指数分布参数的Bayes估计[J].应用概率统计，2001，17(3)：229-235.
[6] 龙兵，周良泽.定数截尾数据缺失场合下冷贮备串联系统可靠性指标的经验Bayes估计[J].数学的实践与认识，2011，41(002)：115-121.
[7] 高妮，师义民.一种反延时电路的可靠性评估[J].电子技术应用，2008(6)：77-80.
[8] 罗雯，魏建中，阳辉，等.电子元器件可靠性试验工程[M].北京：电子工业出版社，2005.
[9] PATNAIK P B.The non-central 2 and F-distribution andtheir applications[J].BiomEtrika，1949，36(1)：202-232.
