
0 引言
传统对称加密系统中,验证设备将密钥信息存储在如Flash等非易失性存储器上,然而这种存储方式容易被读取或恶意篡改造成安全隐患。物理不可克隆函数(Physical Unclonable Function,PUF)利用电路在制造过程由工艺造成的差异得到的响应生成加密信息[1],以其不可预测性、不可克隆性有望生成加密设备的硬件“指纹”,解决上述安全问题。近年来国内外对PUF在信息安全上的应用进行了研究[2-4],然而,PUF的响应在复现时由于电压温度等原因往往会产生差异,因此不能直接用来作为密钥使用。
针对PUF响应的稳定性处理,文献[5]提出的择多模块处理方法虽然实现简单,但认证过程没有密钥生成。文献[6]、[7]提出了一种模糊提取器(Fuzzy Extractor,FE)来得到稳定输出,然而这个纠正过程由于辅助数据的公开会产生熵泄露问题带来安全隐患,文献[8]、[9]等对此进行了安全分析。因此,文献[10]提出一种基于IBS(Index-Based Syndrome,IBS)的改进结构,将响应分为长度为L的块,在注册阶段记录每比特值为1的概率,辅助数据发送每比特码字在相应块中发生概率最高的索引值,重现阶段以此决定该块所表示的取值,该方法被证明是无熵泄露的。文献[11]提出了一种VN结构,每两个比特处理PUF响应数据,只使用相邻两比特取值不同时的响应值得到无偏置的效果,从而解决熵泄露问题。然而,这些方法都以舍弃一定的PUF位来减小熵泄露问题,增加了所需的PUF大小,当设备资源受限时这个因素会带来较大负担。
本文通过对传统FE的熵泄露问题进行分析,提出了给PUF响应加入一种人工噪声通道的改进FE结构,并以SRAM PUF为应用背景与其他方法进行比较,表明在PUF大小使用和密钥生成成功率上有一定改善。
1 传统模糊提取器
模糊提取器FE的思想是将有微小变化的数据通过处理进行纠正得到稳定输出,通常由两个阶段构成:(1)注册阶段(enrollment);(2)重现阶段(reconstruction),结构如图1所示[6]。
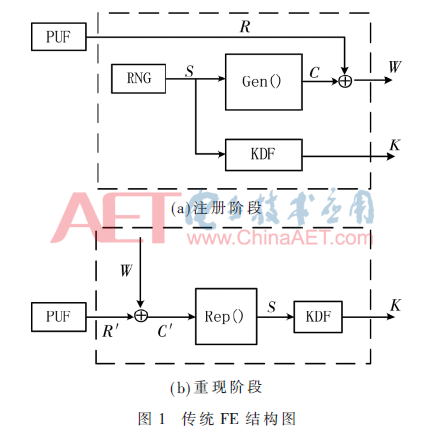
(1)注册阶段:
①随机数发生器产生随机数种子,得到比特串S∈{0,1}。
②S进行KDF运算后得到分布均匀的密钥K。
③同时利用纠错码(例如BCH码等)对S进行Gen()编码生成码字C,将C与PUF响应R进行异或运算得到辅助数据W。
(2)重现阶段:
①辅助数据W与带噪的PUF响应R′进行异或生成C′。
②C′经过相应Rep()译码恢复出随机数种子S。
③对恢复的随机数种子S进行与注册阶段一致的KDF函数生成共享密钥K。
在这个过程中,只要R′与R的汉明距离足够小,满足dis(R,R′)≤t,就可以通过相应纠错编码算法得到原始随机数种子S,最终生成共享密钥。
2 改进的模糊提取器
上述FE结构由于服务器和待验证设备需要利用辅助数据W完成重现,而在通信过程中W对于外界是完全透明的,攻击者可能通过对辅助数据W的抓取分析得到有关随机数种子S的信息进而破解密钥。
令PUF 响应R∈{0,1}n,n为响应长度。为简化分析假设响应R的每比特值服从Ri~(pb,1-pb)分布,其中Pr[Ri=1]=pb,当响应值出现0和1的概率相同(即pb=0.5)时,认为该响应值是无偏的。S是随机数种子,因此看作是满熵的,即H(S)=length(S)=k。采用互信息I(S;W)表示S与W之间的关系强弱,如式(1)所示:

由此可知,当h(pb)≠1时暴露辅助数据W会减小密钥的熵。而通常情况下PUF响应值往往是存在偏置的,因此上述模糊提取器在应用时需要进行改进以解决熵泄露问题。
从上述分析可知,PUF响应值pb≠0.5使得辅助数据W的公开带来熵泄露,因此本文提出在注册阶段通过给响应值R加一个人工噪声通道使得与码字C异或的修正数据R″偏置p′b=0.5。改进后注册阶段的模糊提取器结构如图2所示。
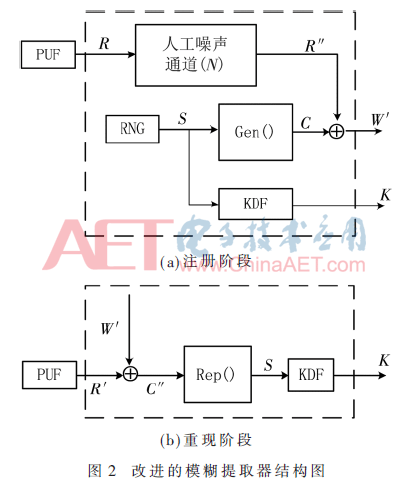


图3为在不同PUF响应的平均错误率e下C″的错误率ε与偏置pb的关系。由图可以看出,当偏置pb与0.5偏差较小时,人工噪声带来的错误率增加量也较小。
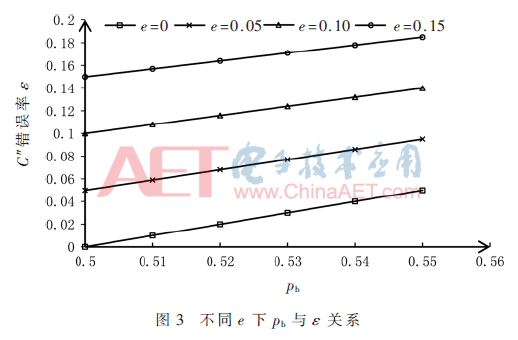
3 结果分析
为将本文提出改进的模糊提取器与其他文献进行对比,采用pb=0.54、e=0.10的SRAM PUF生成128 bit密钥作为应用背景。为降低计算复杂度,系统采用重复编码(Rep)作为内码以及BCH码作为外码。表1为本文所提EF与传统EF、基于C-IBS和VN EF的性能比较。其中,block数量L表示所需的BCH(n,k,t)块个数,取值等于128/k,本文改进后EF的密钥生成失败率计算如下:
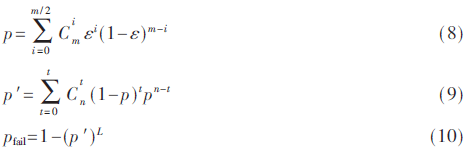
式中,p为重复码译码后的错误率,p′为BCH码译码后的错误率,pfail为L个块后的最终失败率。
从表1中可以看出,传统FE存在较大的熵泄露问题。本文方法与基于C-IBS的模糊提取器相比,在同等SRAM PUF大小条件下所能达到的密钥失败率低了两个量级,与VN FE相比无论从成功率和所需SRAM PUF大小上来说都有一定改善。而且,本文提出的方法只需修改注册阶段的辅助数据生成过程,当服务器等资源计算力受限较小的设备负责完成注册过程时,不会增加待验证设备的计算负担。

4 结论
本文对传统模糊提取器结构的熵泄露问题进行了分析,并以此提出通过给PUF响应加入人工噪声通道以减小偏置,解决因辅助数据公开导致的熵泄露问题,与其他方法相比在PUF大小和密钥生成成功率上都有一定改善,且不会给工作于重现阶段的资源受限设备带来额外操作。下一步可以研究提高纠错效率的方法,减小因引入人工噪声通道带来的错误率增加的影响。
参考文献
[1] RUHRMAIR U,HOLCOMB D E.PUFs at a glance[C].Design,Automation and Test in Europe Conference and Exhibition(DATE).Dresden,Germany,2014:1-6.
[2] 吴缙,徐金甫.基于PUF的可信根及可信计算平台架构设计[J].电子技术应用,2018,44(9):34-38.
[3] SUTAR S,RAHA A,RAGHUNATHAN V.Memory-based combination PUFs for device authentica-tion in embedded systems[J].IEEE Transactions on Multi-Scale Computing Systems,2018,4(4):793-810.
[4] 周恩辉,刘雅娜.基于物理不可克隆函数的高性能RFID网络隐私保护算法[J].电子技术应用,2016,42(3):98-101.
[5] 刘伟强,崔益军,王成华.一种低成本物理不可克隆函数结构的设计实现及其RFID应用[J].电子学报,2016,44(7):1772-1776.
[6] DODIS Y,OSTROVSKY R,REYZIN L,et al.Fuzzy extractors:how to generate strong keys from biometrics and other noisy data[J].SIAM Journal on Computing,2008,38(1):97-139.
[7] MAES R,HERREWEGE A V,VERBAUWHEDE I.PUFKY:a fully functional PUF-based cryptographic key generator[C].International Workshop on Cryptographic Hardware and Embedded Systems.Springer,Berlin,Heidelberg,2012.
[8] ANDRE S,TARAS S,BORIS S,et al.Eliminating leakage in reverse fuzzy extractors[J].IEEE Transactions on Information Forensics and Security,2018,13(4):954-964.
[9] 万超.基于PUF的零信息泄露的安全概略的设计与实现[D].成都:电子科技大学,2018.
[10] YU M D,DEVADAS S.Secure and robust error correction for physical unclonable functions[J].IEEE Design & Test of Computers,2010,27(1):48-65.
[11] MAES R,LEEST V V D,SLUIS E V D,et al.Secure key generation from biased PUFs[M].Cryptographic Hardware and Embedded Systems--CHES 2015.Springer Berlin Heidelberg,2015.
[12] MATTHIAS H,MERLI D,STUMPF F,et al.Complementary IBS:application specific error correction for PUFs[C].IEEE International Symposium on Hardware-oriented Security & Trust.IEEE,2012.
作者信息:
潘畲稣1,2, 张继军1,张钊锋2
(1.上海大学 材料科学与工程学院,上海201900;2.中国科学院上海高等研究院,上海200120)